In
the post (Setup time and hold time – static timing analysis), we introduced setup and
hold timing requirements and also discussed why these requirements exist. In this post, we will be discussing how these checks are applied
for different cases for paths starting from and ending at flip-flops.
In present day designs, most of the paths (more than 95%) start from and end at flip-flops (exceptions are there like paths starting from and/or ending at latches). There can be flops which are positive edge triggered or negative edge triggered. Thus, depending upon the type of launching flip-flop and capturing flip-flop, there can be 4 cases as discussed below:
1)
Setup
and hold checks for paths launching from positive edge-triggered flip-flop and
being captured at positive edge-triggered flip-flop (rise-to-rise checks): Figure 1 shows a
path being launched from a positive edge-triggered flop and being captured on a
positive edge-triggered flop. In this case, setup check is on the next rising
edge and hold check is on the same edge corresponding to the clock edge on
which launching flop is launching the data.
 |
|
Figure 1 : Timing path from positive
edge flop to positive edge flop (rise to rise path)
|
Figure 2 below shows the setup and hold checks for positive edge-triggered register to positive edge-triggered register in the form of waveform. As is shown,
setup check occurs at the next rising edge and hold check occurs at the same
edge corresponding to the launch clock edge. For this case setup timing equation cab be given as:
Tck->q
+ Tprop + Tsetup < Tperiod + Tskew (for setup check)
And the equation for hold timing can be given as:
And the equation for hold timing can be given as:
Tck->q
+ Tprop > Thold + Tskew (for
hold check)
Where
Tck->q : Clock-to-output delay of launch register
Tprop : Maximum delay of the combinational path between launch and capture register
Thold : Hold time requirement of capturing register
Tskew : skew between the two registers (Clock arrival at capture register - Clock arrival at launch register)
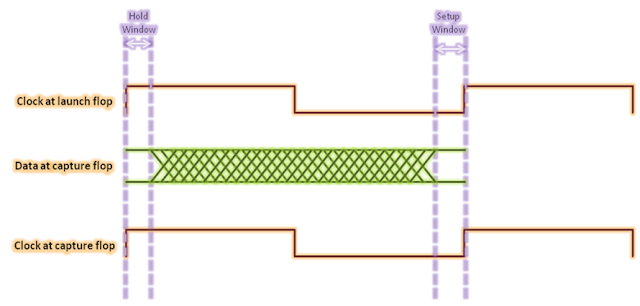
Also, we show below the
data valid and invalid windows. From this figure,
Data valid window = Clock period
– Setup window – Hold window
Start of data valid window = Tlaunch + Thold
End of data valid window = Tlaunch + Tperiod – Tsetup
Start of data valid window = Tlaunch + Thold
End of data valid window = Tlaunch + Tperiod – Tsetup
In other words, data at the input of capture register can toggle any time between (Tlaunch + Thold) and (Tlaunch + Tperiod – Tsetup).
 |
|
Figure 3: Figure showing data valid
window for rise-to-rise path
|
2) Setup
and hold checks for paths launching from positive edge-triggered flip-flop and
being captured at negative edge-triggered flip-flop: In this case, both
setup and hold check are half cycle checks; setup being checked on the next
falling edge at the capture flop and hold on the previous falling edge of clock
at the capture flop (data is launched at rising edge). Thus, with respect to
(case 1) above, setup check has become tight and hold check has relaxed.
 |
|
Figure 4: Timing path from positive
edge flop to negative edge flop (Rise-to-fall path)
|
Figure 5 below shows the setup and hold checks
in the form of waveforms. As is shown, setup check occurs at the next falling edge
and hold check occurs at the previous falling edge corresponding to the launch
clock edge. The equation for setup check can be written, in this case, as:
Tck->q
+ Tprop + Tsetup < (Tperiod/2) + Tskew (for setup check)
And the equation for hold check can be written as:
Tck->q + Tprop + (Tperiod/2) > Thold + Tskew (for hold check)
Tck->q + Tprop + (Tperiod/2) > Thold + Tskew (for hold check)
 |
|
Figure 5: Setup and hold checks for
rise-to-fall paths
|
Also, we show below the
data valid and invalid windows. From this figure,
Data valid window = Clock period
– Setup window – Hold window
Start of data valid window = Tlaunch
– (Tperiod/2)+ Thold
End of data valid window = Tlaunch
+ (Tperiod/2) – Tsetup
As we can see, the data valid window is spread evenly
on both sides of launch clock edge.
3)
Setup
and hold checks for paths launching from negative edge-triggered flip-flop and
being captured at positive edge-triggered flip-flop (rise-to-fall paths):
This case is similar to case 2; i.e. both setup and hold checks are half cycle
checks. Data is launched on negative edge of the clock, setup is checked on the
next rising edge and hold on previous rising edge of the clock.
 |
|
Figure 7: Timing path from negative
edge flop to positive edge flop (fall-to-rise path)
|
Figure
8 below shows the setup and hold checks in the form of waveforms. As is shown,
setup check occurs at the next rising edge and hold check occurs at the
previous rising edge corresponding to the launch clock edge. The equation for setup check can be written, in this case, as:
Tck->q + Tprop + Tsetup < (Tperiod/2) + Tskew (for setup check)
And the equation for hold check can be written as:
Tck->q + Tprop + (Tperiod/2) > Thold + Tskew (for hold check)
Tck->q + Tprop + (Tperiod/2) > Thold + Tskew (for hold check)
 |
|
Figure 8: Setup and hold checks for
fall to rise paths
|
Also, we show below the
data valid and invalid windows. From this figure,
Data valid window = Clock
period – Setup window – Hold window
Start of data valid window = Tlaunch
– (Tperiod/2)+ Thold
End of data valid window = Tlaunch
+ (Tperiod/2) – Tsetup
In this case too, data valid window spreads evenly on
both the sides of launch clock edge.
4)
Setup
and hold checks for paths launching from negative edge-triggered flip-flop and
being captured at negative edge-triggered flip-flop (fall-to-fall paths):
The interpretation of this case is similar to case 1. Both launch and
capture of data happen at negative edge of the clock. Figure 10 shows a path
being launched from a negative edge-triggered flop and being captured on a
negative edge-triggered flop. In this case, setup check is on the next falling
edge and hold check is on the same edge corresponding to the clock edge on
which launching flop is launching the data.
 |
|
Figure 10: Path from negative edge flop
to negative edge flop (fall to fall path)
|
Figure
below shows the setup and hold checks in the form of waveforms. As is shown,
setup check occurs at the next falling edge and hold check occurs at the same
edge corresponding to the launch clock edge.
The equation for setup check can be given as:
The equation for setup check can be given as:
Tck->q
+ Tprop + Tsetup < Tperiod + Tskew (for setup check)
And the equation for hold check can be given as:
And the equation for hold check can be given as:
Tck->q + Tprop > Thold
+ Tskew (for
hold check)
 |
|
Figure 11: Setup and hold check for fall-to-fall path
|
Also, we show below the
data valid and invalid windows. From this figure,
Data valid window = Clock period
– Setup window – Hold window
Start of data valid window = Tlaunch
+ Thold
End of data valid window = Tlaunch
+ Tperiod – Tsetup




Can you please explain what is this "T launch" time period explained in the above equations?
ReplyDeleteHi
DeleteIt is clock latency at the launch flip-flop.
Can you please tell how Tperiod/2 is included in the hold time equation of case 2?
ReplyDeleteThis is because capture edge where hold is being checked is T/2 time behind launch edge.
Deletefor posedgeflop to negedge flop, why is it half cycle for setup check? and not 1.5cycle? I was using the logic from this https://vlsiuniverse.blogspot.com/2018/07/is-hold-always-checked-on-same-edge.html
ReplyDeletelaunch at first posedge (stage k), the k+1 on negative edge doesn't occur until 1.5cycle isn't it?
Hi Vignesh
DeleteGood question, that actually meant that if both edges are involved in a timing check, then count each edge (either positive or negative as 1); This essentially makes the next negative edge k+1th edge. Can you read it again and let me know. If it does not make sense, can you suggest edits to that post for the benefit of others. Thanks a lot for your feedback. :-)
Why is the launch edge shown on next state for positive to positive while it is on the current edge for positive to negative FF?
ReplyDeleteThough you show the launch edge on the next edge for a Positive to positive FF, your data validity window in written with respect to the edge on which hold is checked(K). Why?
Static timing analysis always checks worst cases.
DeletePositive to positive : Launch on Kth edge. capture should be on next rise edge. so K+1. From clock period perspective you are getting complete cycle
Positive to negative : these are 2 different edges. from clock perspective you get only half cycle. So launch and capture happen in same cycle but different edges.