Setup checks and hold checks for latch-to-flop timing paths

There can be 4 cases of latch-to-flop timing paths as discussed below:

1. Positive level-sensitive latch to positive edge-triggered register: Figure 1 below shows a timing path being launched from a positive level-sensitive latch and being captured at a positive edge-triggered register. In this case, setup check will be full cycle with zero-cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 1: Positive level-sensitive latch to positive edge-triggered register timing path

Timing waveforms corresponding to setup check and hold check for a timing path from positive level-sensitive latch to positive edge-triggered register is as shown in figure 2 below.

Figure 2: Setup and hold check waveform for positive latch to positive register timing path

2. Positive level-sensitive latch to negative edge-triggered register: Figure 3 below shows a timing path from a positive level-sensitive latch to negative edge-triggered register. In this case, setup check will be half cycle with half cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 3: A timing path from positive level-sensitive latch to negative edge-triggered register

Timing waveforms corresponding to setup check and hold check for timing path starting from positive level-sensitive latch and ending at negative edge-triggered register is shown in figure 4 below:

Figure 4: Setup and hold check waveform for timing path from positive latch to negative register

3. Negative level-sensitive latch to positive edge-triggered register: Figure 5 below shows a timing path from a negative level-sensitive latch to positive edge-triggered register. Setup check, in this case, as in case 2, is half cycle with half cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 5: Timing path from negative level-sensitive latch to positive edge-triggered register

Timing waveforms for path from negative level-sensitive latch to positive edge-triggered flop are shown in figure 6 below:

Figure 6: Waveform for setup check and hold check corresponding to timing path from negative latch to positive flop

4. Negative level-sensitive latch to negative edge-triggered register: Figure 7 below shows a timing path from negative level-sensitive latch from a negative edge-triggered register. In this case, setup check will be single cycle with zero cycle hold check. Time borrowed by previous stage will be subtracted from present stage.

Figure 7: Timing path from negative latch to negative flop

Figure 8 below shows the setup check and hold check waveform from negative level-sensitive latch to negative edge-triggered flop.

Figure 8: Timing waveform for path from negative latch to negative flip-flop

Time borrowing in latches

What is time borrowing: Latches exhibit the property of being transparent when clock is asserted to a required value. In sequential designs, using latches can enhance performace of the design. This is possible due to time borrowing property of latches. We can define time borrowing in latches as follows:

Time borrowing is the property of a latch by virtue of which a path ending at a latch can borrow time from the next path in pipeline such that the overall time of the two paths remains the same. The time borrowed by the latch from next stage in pipeline is, then, subtracted from the next path's time.

The time borrowing property of latches is due to the fact that latches are level sensitive; hence, they can capture data over a range of times than at a single time, the entire duration of time over which they are transparent. If they capture data when they are transparent, the same point of time can launch the data for the next stage (of course, there is combinational delay from data pin of latch to output pin of latch).

Let us consider an example wherein a negative latch is placed between two positive edge-triggered registers for simplicity and ease of understanding. The schematic diagram for the same is shown in figure 1 below:

Figure 1: Negative level-sensitive latch between two positive edge-triggered registers

Figure 2 below shows the clock waveform for all the three elements involved. We have labeled the clock edges for convenience. As is shown, latB is transparent during low phase of the clock. RegA and RegC (positive edge-triggered registers) can capture/launch data only at positive edge of clock; i.e., at Edge1, Edge3 or Edge5. LatB, on other hand, can capture and launch data at any instant of time between Edge2 and Edge3 or Edge4 and Edge5.

Figure 2: Clock waveforms

The time instant at which data is launched from LatB depends upon the time at which data launched from RegA has become stable at the input of latB. If the data launched at Edge1 from RegA gets stable before Edge2, it will get captured at Edge2 itself.  However, if the data is not able to get stable, even then, it will get captured. This time, as soon as the data gets stable, it will get captured. The latest instant of time this can happen is the latch closing edge (Edge3 here). One point here to be noted is that at whatever point data launches from LatB, it has to get captured at RegC at edge3. The more time latch takes to capture the data, it gets subtracted from the next path. The worst case setup check at latB is at edge2. However, latch can borrow time as needed. The maximum time borrowed, ideally, can be upto Edge3. Figure 3 below shows the setup and hold checks with and without time borrow for this case:

Figure 3: Setup check with and without time borrow

The above example consisted of a negative level-sensitive latch. Similarly, a positive level-sensitive latch will also borrow time from the next stage, just the polarities will be different.

Also read:

• Metastability
• Lockup latch - principle, application and timing
• Setup check and hold check for register to latch timing paths
• False paths - basics and example scenarios
• Can hold be frequency dependent

Setup check and hold check for flop-to-latch timing paths

In the post (Setup and hold – basics of timinganalysis), we introduced setup and hold timing requirements and also discussed why these requirements are needed to be applied. In this post, we will be discussing how these checks are applied for different cases for paths starting from flops and ending at latches and vice-versa.

Present day designs are focused mainly on the paths between flip-flops as the elements dominating in them are flip-flops. But there are also some level-sensitive elements involved in data transfer in current-day designs. So, we need to have knowledge of setup and hold checks for flop-to-latch and latch-to-flop paths too. In this post, we will be discussing the former case. In totality, there can be total 4 cases involved in flop-to-latch paths as discussed below:

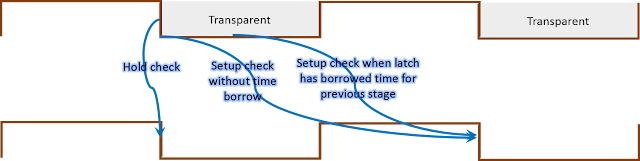
1)                  Paths launching from positive edge-triggered flip-flop and being captured at positive level-sensitive latch: Figure 1 shows a path being launched from a positive edge-triggered flop and being captured on a positive level-sensitive latch. In this case, setup check is on the same rising edge (without time borrow) and next falling edge (with time borrow) and hold check on the previous falling edge with respect to the edge at which data is launched by the launching flop.

Figure 1: Timing path from positive edge flop to positive level latch

Figure below shows the waveforms for setup and hold checks in case of paths starting from a positive edge triggered flip-flop and ending at a positive level sensitive latch. As can be figured out, setup and hold check equations can be described as:

            T_ck->q + T_prop + T_setup < T_skew + T_{period/2                                (for setup check)}

            T_ck->q + T_prop > T_hold + T_skew    - (T_period/2)                       _{(for hold check)}

2)                  Paths launching from positive edge-triggered flip-flop and being captured at negative level-sensitive latch: Figure 3 shows a path starting from positive edge-triggered flip-flop and being captured at a negative level sensitive latch. In this case, setup check is on the next falling edge (without time borrow) and on next positive edge (with time borrow). Hold check on the same edge with respect to the edge at which data is launched (zero cycle hold check).

 

Figure 3: Path from positive edge flop to negative level latch

Figure below shows the waveforms for setup and hold checks in case of paths starting from a positive edge triggered flip-flop and ending at a negative level-sensitive latch. As can be figured out, setup and hold check equations can be described as:

            T_ck->q + T_prop + T_setup < (T_period) + T_{skew                        (for setup check)}

            T_ck->q + T_prop > T_hold + T_{skew                                                   (for hold check)}

 

3)                  Paths launching from negative edge-triggered flip-flop and being captured at positive level-sensitive latch: Figure 5 shows a path starting from negative edge-triggered flip-flop and being captured at a positive level sensitive latch. In this case, setup check is on the next rising edge (without time borrow) and next falling edge (with time borrow). Hold check on the next rising edge with respect to the edge at which data is launched.

 

Figure 5: Path from negative edge flop to positive level latch

Figure below shows the waveforms for setup and hold checks in case of paths starting from a negative edge triggered flip-flop and ending at a positive level-sensitive latch. As can be figured out, setup and hold check equations can be described as:

            T_ck->q + T_prop + T_setup < (T_period) + T_{skew                        (for setup check)}

            T_ck->q + T_prop > T_hold + T_{skew                                                   (for hold check)}

1)                  Paths launching from negative edge-triggered flip-flop and being captured at negative level-sensitive latch: Figure 5 shows a path starting from negative edge-triggered flip-flop and being captured at a negative level sensitive latch. In this case, setup check is on the same edge (without time borrow) and on next rising edge (with time borrow). Hold check on the next rising edge with respect to the edge at which data is launched.

 

Figure 5: Path from negative edge flop to negative level latch

Figure below shows the waveforms for setup and hold checks in case of paths starting from a negative edge triggered flip-flop and ending at a negative level-sensitive latch. As can be figured out, setup and hold check equations can be described as:

            T_ck->q + T_prop + T_setup < T_period/2 + T_{skew                             (for setup check)}

            T_ck->q + T_prop > T_hold + T_skew   - (T_period/2)                       _{(for hold check)}