Regions of operation of MOS transistors

A Metal Oxide Semiconductor Field Effect Transistors (MOSFET, or simply, MOS) is a four terminal device. Figure 1 below shows the general representation of an N-MOS (for PMOS, simply replace N regions with P and vice-versa). MOS is a Voltage-controlled current source as the current through MOS is a function of relative voltage levels of its terminals. The relative voltages of gate, drain and source terminals (assuming bulk or substrate to be at same voltage as source) determine the magnitude of current flowing in MOS. In each of these regions, we can represent the current as a function of gate-to-source voltage (V_GS) and drain-to-source voltage (V_DS).

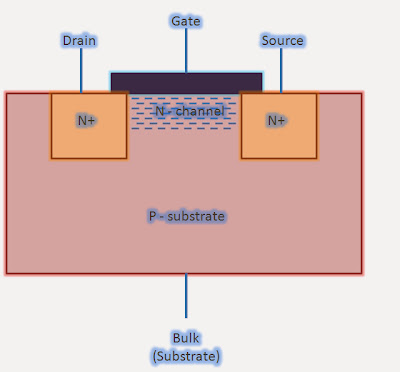MOS transistor - a 4-transistor device

In a MOS device, the current flows on formation of channel of carriers between source and drain terminals. For this, voltage at gate terminal needs to be such that it attracts carriers of appropriate type towards itself. When sufficient carriers are attracted towards gate, channel is said to be formed. A current, then, flows between source and drain terminals depending upon the voltage levels of these terminals. The voltage level of substrate also impacts the magnitude of current as it also determines the level of carriers in the channel.

For an N-MOS device, the channel is formed by electrons. So, to attract electrons, gate voltage must be greater than source voltage. For the formation of channel, the difference between V_G and V_S (V_G – V_S) must be greater than V_th (threshold voltage of the MOS).

Threshold voltage is defined as the minimum difference in gate-to-source voltage needed for the formation of channel in a MOS device. For NMOS, V_th is positive as for channel formation gate needs to be at higher voltage as explained above. Similarly, for PMOS, V_th is negative as gate needs to be at lower voltage than source for channel to be formed.

On increasing gate voltage beyond threshold voltage, current through MOS increases with increasing gate voltage. Also, if we increase drain voltage keeping gate voltage constant, current increases till a particular drain voltage. After that, increasing drain voltage does not affect the current. Depending upon the relative voltages of its terminals, MOS is said to operate in either of the cut-off, linear or saturation region.

• Cut off region – A MOS device is said to be operating when the gate-to-source voltage is less than V_th. Thus, for MOS to be in cut-off region, the necessary condition is –

0 < V_GS < V_th                           -                       for NMOS

0 > V_GS > V_{th                                    -}                           for PMOS (as threshold voltage of PMOS is negative)

Cut-off region is also known as sub-threshold region. In this region, the dependence of current on gate voltage is exponential. The magnitude of current flowing through MOS in cut-off region is negligible as the channel is not present. The conduction happening in this region is known as sub-threshold conduction.

• Linear or non saturation region – For an NMOS, as gate voltage increases beyond threshold voltage, channel is formed between source and drain terminals. Now, if there is voltage difference between source and drain, current will flow. The magnitude of current increases linearly with increasing drain voltage till a particular drain voltage determined by the following relations –

V_GS ≥ V_th

V_DS < V_GS – V_th

The current is, then, represented as a linear function of gate-to-source and drain-to-source voltages. That is why, MOS is said to be operating in linear region. The linear region voltage-current relation is given as follows:

Id(Linear) = µ Cox W/L (Vgs – Vth – Vds/2) Vds.

            

Similarly, for P-MOS transistor, condition for P-MOS to be in linear region is represented as:

                        V_GS < V_th                        OR                         V_SG > |V_th|

            And      V_DS > V_GS + V_th                           OR             V_SD < V_SG - |V_th| 

• Saturation Region – For an NMOS, at a particular gate and source voltage, there is a particular level of voltage for drain, beyond which, increasing drain voltage seems to have no effect on current. When a MOS operates in this region, it is said to be in saturation. The condition is given as:

V_GS ≥ V_th

V_DS > V_GS – V_th

            The current, now, is a function only of gate and source voltages:

                        Id(saturation) = µ Cox W/L (Vgs – Vth – Vds/2)²

Also read:

• Latch-up in CMOS devices
• Transmission gates
• Why depletion MOSFET cannot be used to create negative logic
• Defining a clock signal in VHDL