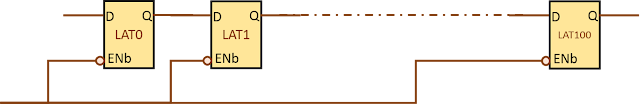How clock gating reduces power dissipation

As discussed in clock gating - basics, enable signal coming in data path is transferred into clock path in order to save dynamic power. But the question is exactly how is this power saved. In this post, we will discuss the same. 

A flip-flop implemented as a standard cell mostly has two internal inverters to generate clk' and clk_delay signals. So, even if the flip-flop input is kept constant, there is still toggling of data at these inverters, thereby dissipating dynamic power. In addition to this, there is internal power dissipation inside flip-flop due to charging and discharging of transistors' gates repetitively because of clock toggling, but this component is not a significant factor compared to dynamic power of inverters. Figure 2 below shows the internal structure of flip-flop, which has two latches in master-slave configuration and two inverters in clock path.

Figure 2: Flip-flop internal structure

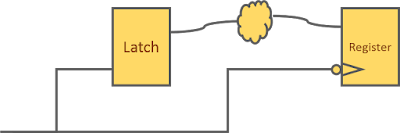
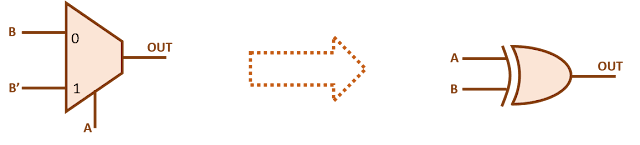
Every clock cycle, these two inverters toggle regardless of flip-flop output toggling. However, implementation of clock gating will prohibit the toggling of these inverters when data is not toggling. Let us assume that a latch-based ICG is inserted. Thus, a mux in data path is replaced by an ICG in clock path. But there is a difference here. If there are, say 1000, flip-flops with same enable signal, there will be a common ICG inserted for these. Thus, instead of now 2000 inverters (inside 1000 flops) toggling when flip-flop output will be constant, we have only 2 inverters inside ICG consuming dynamic power. This is how dynamic power is saved. However, if only 1 flop had been clock gated in this manner, there would not have been any dynamic power saving, instead we have an ICG instead of a latch, it may result in overall loss in terms of area and power.

Whether there is any net saving is governed by how many flips-flops have been clock gated using a single ICG.

Also, as discussed, many muxes in data path with same enable are replaced by an ICG in clock path. Thus, there are advantages in terms of area and leakage power too, in addition to dynamic power.

Design query : How can we construct a 101 non overlapping counter using only combinational circuit for 32 bit input for example on considering 10101001 i want an output as 1 since there is only 1 101 non overlapping sequence

Solution: The design in question is a combinatorial design with 32-bit input (given) and a 4-bit output as shown in figure 1 below. How the output is 4-bit is a bit tricky. For this, we have to understand the problem. We have to count the number of non-overlapping "101" sequences in 32-bit input. Thus, "10101" counts as only a single occurrence, and "101101" counts as two occurrences. So, the maximum number of such patterns will occur when "101101" is repeated, which comes out to be 10 in a 32-bit number. 10 can be represented by a 4-bit number.

Figure 1: Design representation

One of the solutions, of course is to make a truth-table and then find a solution using logic equation solving. But the number of combinations possible here is huge and practically impossible to find a solution. So, we need to follow a modular approach here.

We can divide the problem into two parts, detecting the required pattern and then counting how many patterns actually were detected. We are introducing an intermediate 32-bit output, each bit (Nth bit) detecting if the pattern was found with Nth bit of input as the middle symbol of pattern. To detect non-overlapping "101" pattern, we need to look into 2 bits on each side, thereby making a combinational logic comprising of 7 bits. There will be special cases for terminal bits (here bit-0, bit-1, bit-30 and bit-31) where we know that there are less than 2 bits on one side. So, we need to have special logic for these bits.

The overall combinational logic will look like as shown in figure below. Int-N (Nth bit of intermediate output) is a resultant of (Bit-N-3 to Bit-N+3). The number of 1's in the intermediate output will tell how many patterns were detected, which, as discussed earlier, will be maximum 10.

Figure 2: Block diagram representation of design

Let us, now, proceed for a generic logic for Nth intermediate output. As discussed, Nth output (On) depends upon 7 bits, 3 bits on the up and 3 on down. The Nth bit of output will show "1"only for following cases: X1101XX & 00101XX. As 10101XX will be detected as "1" for N+2 bit of output. If we denote the variables involved as G,F,E,D,C,A, then the output expression becomes

On = FED'C + G'F'ED'C

On = ED'C (F+G')

 For bit 31, the upper two bits do not exist. 101XX is the expression for getting output as 1. Thus, the equation, on a similar note, can be expressed as:

O31 = ED'C

For bit 30, the expression comes out to be X101XX. So, O30 also has same logic as O31.

For O1 and O0, we get the same expression as we get for On. The logic diagram for obtaining intermediate outputs is shown in figure 3 below:

Figure 3: Circuit with logic for intermediate output

Now, we have got the intermediate outputs showing which bits have the specified pattern detected. The number of "1"in the final output is our final answer. So, we need a special circuit to count the number of 1's combinationally in a bus as shown in figure 3 above. "Combinationally count number of 1's in a bus" explains how we can do this.

This post is in response to a query posted on our "post your query" page. In case you want to have an answer to your query, you can post a comment. We will try our best to answer.

Design query :: Combinationally count number of 1's in a 32-bit bus

Solution: The design in question is a combinational design with 32-bit input and 6-bit output as there can be maximum 32 1's and 32 stands "100000" in binary. Making a truth-table or K-map for this problem is not practical, so we have to take a modular approach. Let us divide the problem into detecting number of 1's among 4 bits and then adding the resulting numbers together providing the total count.

Let us first create a truth-table converting the number of 1's in a 4-bit stream into a 2-bit number. The resulting truth table is shown in figure 1.

Figure 1: Truth table for 4-bit count 1's circuit

Solving the above for O2, O1 and O0 using K-maps, we get the expressions as shown in figures 2, 3 and 4 below.

Figure 2: Expression for O2

Figure 3: Expression for O1

Figure 4: Expression for O0

Thus, we have 8 instances, each counting the number of ones pertaining to respective 4 bits. The next thing we need is to add these 8 three-bit numbers to obtain the resultant total number of 1's in the 32-bit number we got. For this, we can again follow modular approach to add two numbers at a time until we are left with a single number. The block diagram of the complete solution is shown below in figure 5.

Figure 5: Complete block diagram of counting number of 1's

Divide by 2 clock in VHDL

Clock dividers are ubiquitous circuits used in every digital design. A divide-by-N divider produces a clock that is N times lesser frequency as compared to input clock. A flip-flop with its inverted output fed back to its input serves as a divide-by-2 circuit. Figure 1 shows the schematic representation for the same.

Divide by 2 clock circuit

                                          

Following is the code for a divide-by-2 circuit.

-- This module is for a basic divide by 2 in VHDL.

library ieee;

use ieee.std_logic_1164.all;

entity div2 is

                port (

                                reset : in std_logic;

                                clk_in : in std_logic;

                                clk_out : out std_logic

                );

end div2;

-- Architecture definition for divide by 2 circuit

architecture behavior of div2 is
signal clk_state : std_logic;

begin

                process (clk_in,reset)

                begin

                                if reset = '1' then

                                                clk_state <= '0';

                                elsif clk_in'event and clk_in = '1' then

                                                clk_state <= not clk_state;

                                end if;

                end process;
clk_out <= clk_state;

end architecture;

Hope you’ve found this post useful. Let us know what you think in the comments.

Programming problem: Synthsizable filter design in C++

Problem statement: Develop a synthesizable C/C++ function which is capable of performing image filtering. The filtering operation is defined by following equation:

// B -> filtered image

// A -> Input image

// h -> filter coefficients

int filter_func() {

                const int L = 1;

                const int x_size = 255;

                const int y_size = 255;

                int A_image[x_size][y_size];

                int B_image[x_size][y_size];

                int h[2*L+1][2*L+1];

                // Initializing the filtered image

                for (int i = 0; i < x_size; i++) {

                                for (int j = 0; j < y_size; j++) {

                                                B_image[i][j] = 0;

                                }

                }

                for (int i = 0; i < x_size; i++) {

                                for (int j = 0; j < y_size; j++) {

                                                for (int l = -L; l <= L; l++) {

                                                                for (int k = -L; k <= L; k++) {

                                                                                B_image[i][j] = B_image[i][j] + A_image[i-k][j-l]*h[k+L][l+L];

                                                                }

                                                }

                                }

                }

}

Hope you’ve found this post useful. Let us know what you think in the comments.

Technology scaling factor

For instance, you will find technology nodes as 180 um 90 um, 65 um, 45 um, 32 um, 22 um and so on..

*Source - Digital integrated circuits - A design perspective by Jan M Rabay

Setup checks and hold checks for latch-to-flop timing paths

There can be 4 cases of latch-to-flop timing paths as discussed below:

1. Positive level-sensitive latch to positive edge-triggered register: Figure 1 below shows a timing path being launched from a positive level-sensitive latch and being captured at a positive edge-triggered register. In this case, setup check will be full cycle with zero-cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 1: Positive level-sensitive latch to positive edge-triggered register timing path

Timing waveforms corresponding to setup check and hold check for a timing path from positive level-sensitive latch to positive edge-triggered register is as shown in figure 2 below.

Figure 2: Setup and hold check waveform for positive latch to positive register timing path

2. Positive level-sensitive latch to negative edge-triggered register: Figure 3 below shows a timing path from a positive level-sensitive latch to negative edge-triggered register. In this case, setup check will be half cycle with half cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 3: A timing path from positive level-sensitive latch to negative edge-triggered register

Timing waveforms corresponding to setup check and hold check for timing path starting from positive level-sensitive latch and ending at negative edge-triggered register is shown in figure 4 below:

Figure 4: Setup and hold check waveform for timing path from positive latch to negative register

3. Negative level-sensitive latch to positive edge-triggered register: Figure 5 below shows a timing path from a negative level-sensitive latch to positive edge-triggered register. Setup check, in this case, as in case 2, is half cycle with half cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 5: Timing path from negative level-sensitive latch to positive edge-triggered register

Timing waveforms for path from negative level-sensitive latch to positive edge-triggered flop are shown in figure 6 below:

Figure 6: Waveform for setup check and hold check corresponding to timing path from negative latch to positive flop

4. Negative level-sensitive latch to negative edge-triggered register: Figure 7 below shows a timing path from negative level-sensitive latch from a negative edge-triggered register. In this case, setup check will be single cycle with zero cycle hold check. Time borrowed by previous stage will be subtracted from present stage.

Figure 7: Timing path from negative latch to negative flop

Figure 8 below shows the setup check and hold check waveform from negative level-sensitive latch to negative edge-triggered flop.

Figure 8: Timing waveform for path from negative latch to negative flip-flop

2-input gates using 2:1 mux

Definition of a multiplexer: A 2^n-input mux has n select lines. It can be used to implement logic functions by implementing LUT (Look-Up Table) for that function. A 2-input mux can implement any 2-input function, a 4-input mux can implement any 3-input, an 8-input mux can implement any 4-input function, and so on. This property of muxes makes FPGAs implement programmable hardware with the help of LUT muxes. In this post, we will be discussing the implementation of 2-input AND, OR, NAND, NOR, XOR and XNOR gates using a 2-input mux.

2-input AND gate implementation using 2:1 mux: Figure 1 below shows the truth table of a 2-input AND gate. If we observe carefully, OUT equals '0' when A is '0'. And OUT follows B when A is '1'. So, if we connect A to the select pin of a 2:1 mux, AND gate will be implemented if we connect D0 to '0' and D1 to 'B'.

Figure 1: Truth table of AND gate

Figure 2 below shows the implementation of 2-input AND gate using a 2:1 multiplexer.

Figure 2: Implementation of AND gate using a 2:1 mux

2-input NAND gate using 2:1 mux: Figure 3 below shows the truth table of a 2-input NAND gate. If we observe carefully, OUT equals '1' when A is '0'. Similarly, when A is '1', OUT is B'. So, if we connect SEL pin of mux to A, D0 pin of mux to '1' and D1 to B', then it will act as a NAND gate.

Figure 3: Truth table of 2-input NAND gate

Figure 4 below shows the implementation of a 2-input NAND gate using 2:1 mux.

Figure 4: Implementation of 2-input NAND gate using 2:1 mux

2-input OR gate using 2x1 mux: Figure 5 below shows the truth table for a 2-input OR gate. If we observe carefully, OUT equals B when A is '0'. Similarly, OUT is '1' (or A), when A is '1'. So, we can make a 2:1 mux act like a 2-input OR gate, if we connect D0 pin to B and D1 pin to A, with select connected to A.

Figure 5: Truth table of 2-input OR gate

Figure 6 below shows the implementation of 2-input OR gate using a 2:1 multilpexer:

Figure 6: Implementation of 2-input OR gate using 2:1 mux

2-input NOR gate using 2x1 mux: Figure 7 below shows the truth table of a 2-input NOR gate. If we observe carefully, OUT equal B' when A is '0'. Similarly, OUT equals '0' when A is '1'. So, we can make a 2-input mux act like a 2-input NOR gate, if we connect SEL of mux to A, D0 to B' and D1 to '0'.

Figure 7: Truth table of 2-input NOR gate

Figure 8 shows the implementation of 2-input NOR gate using 2:1 mux.

Figure 8: Implementation of 2-input NOR gate using 2x1 mux

2-input XNOR gate using 2x1 mux: Figure 9 below shows the truth table of a 2-input XNOR gate. If we observe carefully, OUT equals B' when A is '0' and equals B when A is '1'. So, a 2-input XNOR gate can be implemented from a 2x1 mux, if we connect SEL pin to A, D0 to B' and D1 to B.

Figure 9: Truth table of 2-input XNOR gate

The implementation of 2-input XOR gate using a 2x1 mux is as shown in figure 10.

Figure 10: Implementation of 2-input XNOR gate using 2x1 mux

2-input XOR gate using 2x1 mux: Figure 11 shows the truth table for a 2-input XOR gate. If we observe carefully, OUT equals B when A is '0' and B' when A is '1'. So, a 2:1 mux can be used to implement 2-input XOR gate if we connect SEL to A, D0 to B and D1 to B'.

Figure 11: Truth table of 2-input XOR gate

Figure 12 shows the implementation of 2-input XOR gate using 2x1 mux.

Implementation of 2-input XOR gate using 2x1 mux

NOT gate using 2:1 mux: Figure 13 shows the truth table for a NOT gate. The only inverting path in a multiplexer is from select to output. To implement NOT gate with the help of a mux, we just need to enable this inverting path. This will happen if we connect D0 to '1' and D1 to '0'.

Figure 13: Truth table of NOT gate

Figure 14 shows the implementation of NOT gate using 2x1 mux:

Figure 14: Implementation of NOT gate using 2x1 mux

Interesting problem – Latches in series

Problem: 100 latches (either all positive or all negative) are placed in series (figure 1). How many cycles of latency will it introduce?

Figure 1 : 100 negative level-sensitive latches in series

As we know, setup check between latches of same polarity (both positive or negative) is zero cycle with half cycle of time borrow allowed as shown in figure 2 below for negative level-sensitive latches:

Figure 2: Setup check between two negative level-sensitive latches

So, if there are a number of same polarity latches, all will form zero cycle setup check with the next latch; resulting in overall zero cycle phase shift.

As is shown in figure 3, all the latches in series are borrowing time, but allowing any actual phase shift to happen. If we have a design with all latches, there cannot be a next state calculation if all the latches are either positive level-sensitive or negative level-sensitive. In other words, for state-machine implementation, there should not be latches of same polarity in series.

Figure 3 : Timing for 100 latches in series

Hope you’ve found this post useful. Let us know what you think in the comments.

Also read:

• Build a latch using a 2:1 multiplexer
• Multicycle paths handling in STA
• Latchup in CMOS devices
• Lockup latch - principle, application and timing
• Data checks - all about data setup and data hold checks

XOR/XNOR gate using 2:1 MUX

2-input XOR gate using a 2:1 multiplexer: As we know, a 2:1 multiplexer selects between two inputs depending upon the value of its select input. The function of a 2:1 multiplexer can be given as:

OUT = IN0 when SEL = 0 ELSE IN1

Also, a 2-input XOR gate produces a ‘1’ at the output if both the inputs have different value; and ‘0’ if the inputs are same. The truth table of an XOR gate is given as:

A	B	OUT
0	0	0
0	1	1
1	0	1
1	1	0

Truth table of XOR gate

In the truth table of XOR gate, if we fix a value, say B, then

OUT = A WHEN B = 0 ELSE A’

Both the above equations seem equivalent if we connect negative of IN0 to IN1 in a multiplexer. This is how a 2:1 multiplexer will implement an XOR gate. Figure 1 below shows the implement of a 2-input XOR gate using a 2:1 Multiplexer.

Implementing a 2-input XOR gate using a 2:1 Multiplexer

I hope you’ve found this post useful. Let me know what you think in the comments. I’d love to hear from you all.

2-input XNOR gate using a 2:1 multiplexer: Similarly, the truth table of XNOR gate can be written as:

A	B	OUT
0	0	1
0	1	0
1	0	0
1	1	1

Truth table of XNOR gate

In the truth table, if we fix, say A, then

OUT = B WHEN A = 1, ELSE B’

Thus, XNOR gate is the complement of XOR gate. It can be implemented if we connect A to IN1 and Abar to IN0.

2-input XNOR gate using 2:1 multiplexer

Read also:

• Build a latch using 2:1 multiplexer
• Clock gating checks at a multiplexer
• Implementing 3 and 4 variable functions using a multiplexer
• Interesting Design problem - BCD multiply by 5 circuit

What is Static Timing Analysis?

Static timing analysis (STA) is an analysis method of computing the max/min delay values of a complete circuit without actually simulating the full circuit. In STA, static delays such as gate delay and net delays are considered in each path. These delays are, then, compared against the required bounds on the delay values and/or the relationship between the delays of different gates. In STA, the circuit to be analyzed is broken down into timing paths consisting of gates, registers and nets connecting these. Normally, timing paths start from and end at registers or chip boundary. Based on origin and termination of data, timing paths can be categorized into four categories:

        1.)    Input to register paths: These paths start at chip boundary from input ports and end at registers

        2.)    Register to register paths: These paths start at register output pin and terminate at register input   pin

        3.)    Register to output paths: These paths start at a register and end at chip boundary output ports

        4.)    Input to output paths: These paths start from chip boundary at input port and end at chip               boundary at output port

Timing path from each start-point to end-point are constrained to have maximum and minimum delays. For example, for register to register paths, each path can take maximum of one clock cycle (minus input/output delay in case of input/output to register paths). The minimum delay of a path is governed by hold timing requirement of the endpoints. Thus, the maximum delay taken by a timing path governs the maximum frequency of operation.

As stated before, Static timing analysis does timing analysis without actually simulating the circuit. The delays of cells are picked from respecting technology libraries. The delays are available in libraries in tabulated form on the basis of input transition and output load, which have been calculated based by simulating the cells for a range of boundary conditions. Net delays are calculated based upon R and C models.

One important characteristic of static timing analysis that must be discussed is that static timing analysis checks the static delay requirements of the circuit without applying any vectors, hence, the delays calculated are the maximum and minimum bounds of the delays that will occur in real application scenarios with vectors applied. This enables the static timing analysis to be fast and inclusive of all the boundary conditions. Dynamic timing analysis, on the contrary, applies input vectors, so is very slow. It is necessary to certify the functionality of the design. Thus, static timing analysis guarantees the timing of the design whereas dynamic timing analysis guarantees functionality for real application specific input vectors.

I hope you’ve found this post useful. Let me know what you think in the comments. I’d love to hear from you all.

Defining a clock signal in VHDL

Defining a clock signal in VHDL

Clock is the backbone of any synchronous design. For test-benches, a clock is the most desired signal as almost every design requires a clock. Going a bit deeper, a clock signal is a binary signal that changes state every few time units. So, defining a clock in VHDL is pretty simple, as shown below in the following code:

                signal my_clock : std_logic;

                process               

                                my_clock <= ‘0’;

                                wait for 5 ns;

                                my_clock = ‘1’;

                                wait for 5 ns;

                end process;

The above code defines a clock of  period 10 ns with 5 ns high time and 5 ns low time, hence, 50% duty cycle. Since, we are assigning a value to my_clock in the code, it can wither be defines as a signal or an output. Most probably, clocks are defined in test-benches, hence, are internal signals. High time and low time don’t always need to be same. You can always define a clock that has different high and low times as shown below:

signal my_clock : std_logic;

                process

                                my_clock <= ‘0’;

                                wait for 8 ns;

                                my_clock = ‘1’;

                                wait for 2 ns;

                end process;

As we can see, now, my_clock has a duty cycle of 80%; i.e. a high time of 80% and a low time of 20%.

Defining a clock in this way, obviously, is not synthesizable as we are using delays in code, and delays cannot be synthesized. Hence, this way of defining a clock can only be used in a test-bench to test a piece of code. If you need to write a synthesizable clock, then you have to use structural coding. The simplest of clock generation circuits is a ring counter (a chain of inverters connected back-to-back), but it will have a variable frequency clock because delay of inverters changes on change in operating conditions.