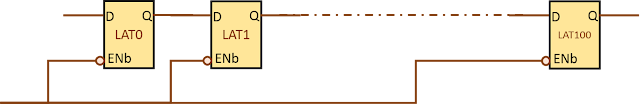Intricacies in handling of half cycle timing paths

What is a half cycle path? A half cycle timing path is one in which launch and capture happen on different clock edges. A half cycle path can be in terms of both setup and hold. However, normally, in technical terms half cycle path is the one which has setup check getting formed as half cycle. For instance, following are some of the examples of half cycle timing paths:

1. A timing path from positive edge-triggered flip-flop to a negative edge-triggered flip-flop and vice-verse. Here, hold check is also half cycle on the previous edge
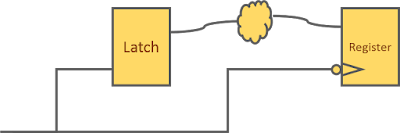
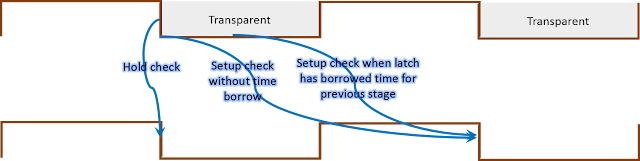
2. A timing path from a positive level-sensitive latch to a negative level-sensitive latch and vice-verse. Here, hold check is zero cycle
3. A timing path from a negative edge-triggered flip-flop forming a clock gating check on AND gate (Here, hold check is zero cycle)
4. A timing path from a positive edge-triggered flip-flop forming a clock gating check on OR gate (here, hold check is zero cycle)

There are also, some cases where hold check is half cycle and setup check is single/zero cycle. These are:

1. A timing path from a negative edge-triggered flip-flop forming a clock gating check on OR gate (Here, setup check is single cycle check)
2. A timing path from a positive edge-triggered flip-flop forming a clock gating check on AND gate (Here, setup check is single cycle check)

In addition, minimu pulse width checks should also be considered same as half cycle timing paths. But, in this case, start-point and end-point are the same register.

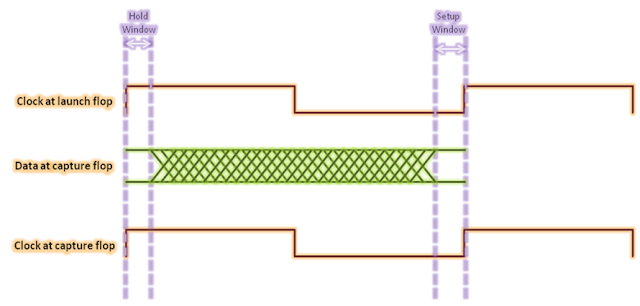
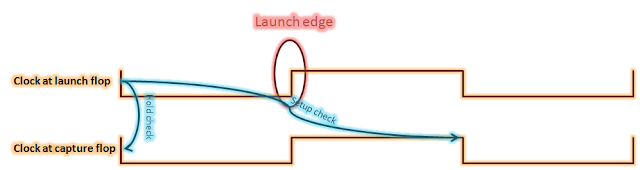
In this post, we will be considering only setup timings paths as example, although the complete discussion applies on all kinds of half cycle setup paths/checks. To start with, let us note down the most simple setup check equation for half cycle timing paths.

T_ck->q + T_prop + T_setup  < (T_period/2) + T_skew

Let us now discuss some of the intricacies that we should be aware of while dealing with half cycle timing paths:

Clock source duty cycle variation: There is always a variation in duty cycle of the clock source due to uncertainty in the relative timings of positive and negative edges. Duty cycle variation is always measured with respect to corresponding positive and negative edges. In other words, we can also say that duty cycle variation is the uncertainty in arrival of negative edge, given that positive edge has arrived at certain fixed point of time. Let us take an example. If we are given a clock with a period of 10 ns with ideal 50% duty cycle. Also, we are given that it has the clock has a duty cycle variation of +-5%. So, if we say that we saw positive edge of clock at 100 ns, we can expect to see negative edge of clock at any time between 14.5 ns and 15.5 ns. Following waveform illustrates this. You can read my earlier post duty cycle variation to have a more detailed elaboration.

So, the setup check equation modifies as:

T_ck->q + T_prop + T_setup  < (T_period/ 2- T_sdc) + T_skew

where T_sdc is the clock source duty cycle variation. Thus, the effective half clock period reduces by an amount equal to duty cycle variation.

Duty cycle degradation:  In addition to source duty cycle variation, there can be assymmetry in rise delay vs fall delay of clock elements. For instance, a buffer may have nominal rise (0 -> 1) delay of 50 ns whereas 48 ns for fall delay (1 -> 0). So, if a clock pulse passes through it, it will eat a portion of this clock pulse as shown in figure 1 below. For more clarity, we have exaggerated the scenario with a fall delay of 30 ns.

So, a half cycle may be larger of smaller than actual half cycle at the clock pin. In the above case, positive to negative edge setup check will be tighter by 20 ns and negative-> positive setup check will be relaxed by same amount (neglective OCVs as of now). So, the modified setup equation, now, becomes:

T_ck->q + T_prop + T_setup  < (T_period/2 - T_sdc) + (T_skew - T_dcd)

As discussed above also, T_dcd can be positive or negative depending upon if rise-fall variation of cells is helping or oppsing.

Can you think of some other scenario that is specific only to half cycle timing paths? Do share, if you do.

Setup checks and hold checks for latch-to-flop timing paths

There can be 4 cases of latch-to-flop timing paths as discussed below:

1. Positive level-sensitive latch to positive edge-triggered register: Figure 1 below shows a timing path being launched from a positive level-sensitive latch and being captured at a positive edge-triggered register. In this case, setup check will be full cycle with zero-cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 1: Positive level-sensitive latch to positive edge-triggered register timing path

Timing waveforms corresponding to setup check and hold check for a timing path from positive level-sensitive latch to positive edge-triggered register is as shown in figure 2 below.

Figure 2: Setup and hold check waveform for positive latch to positive register timing path

2. Positive level-sensitive latch to negative edge-triggered register: Figure 3 below shows a timing path from a positive level-sensitive latch to negative edge-triggered register. In this case, setup check will be half cycle with half cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 3: A timing path from positive level-sensitive latch to negative edge-triggered register

Timing waveforms corresponding to setup check and hold check for timing path starting from positive level-sensitive latch and ending at negative edge-triggered register is shown in figure 4 below:

Figure 4: Setup and hold check waveform for timing path from positive latch to negative register

3. Negative level-sensitive latch to positive edge-triggered register: Figure 5 below shows a timing path from a negative level-sensitive latch to positive edge-triggered register. Setup check, in this case, as in case 2, is half cycle with half cycle hold check. Time borrowed by previous stage will be subtracted from the present stage.

Figure 5: Timing path from negative level-sensitive latch to positive edge-triggered register

Timing waveforms for path from negative level-sensitive latch to positive edge-triggered flop are shown in figure 6 below:

Figure 6: Waveform for setup check and hold check corresponding to timing path from negative latch to positive flop

4. Negative level-sensitive latch to negative edge-triggered register: Figure 7 below shows a timing path from negative level-sensitive latch from a negative edge-triggered register. In this case, setup check will be single cycle with zero cycle hold check. Time borrowed by previous stage will be subtracted from present stage.

Figure 7: Timing path from negative latch to negative flop

Figure 8 below shows the setup check and hold check waveform from negative level-sensitive latch to negative edge-triggered flop.

Figure 8: Timing waveform for path from negative latch to negative flip-flop

Interesting problem – Latches in series

Problem: 100 latches (either all positive or all negative) are placed in series (figure 1). How many cycles of latency will it introduce?

Figure 1 : 100 negative level-sensitive latches in series

As we know, setup check between latches of same polarity (both positive or negative) is zero cycle with half cycle of time borrow allowed as shown in figure 2 below for negative level-sensitive latches:

Figure 2: Setup check between two negative level-sensitive latches

So, if there are a number of same polarity latches, all will form zero cycle setup check with the next latch; resulting in overall zero cycle phase shift.

As is shown in figure 3, all the latches in series are borrowing time, but allowing any actual phase shift to happen. If we have a design with all latches, there cannot be a next state calculation if all the latches are either positive level-sensitive or negative level-sensitive. In other words, for state-machine implementation, there should not be latches of same polarity in series.

Figure 3 : Timing for 100 latches in series

Hope you’ve found this post useful. Let us know what you think in the comments.

Also read:

• Build a latch using a 2:1 multiplexer
• Multicycle paths handling in STA
• Latchup in CMOS devices
• Lockup latch - principle, application and timing
• Data checks - all about data setup and data hold checks

Noise margins

In this realistic world, nothing is ideal. A signal travelling along a wire/cable/transmission line is susceptible to noise from the surroundings. Also, there is degradation in signal due to parasitic elements involved in the line. Moreover, the output signal produced by the transmitter itself only does resemble the ideal signal thereby worsening the scenario. There are repeaters/buffers along the line to minimize the impact of noise. But there is a limit up to which degradation is allowed beyond which the receiver is unable to sense the correct value of the signal. This degradation is measured in terms of noise margins. One can find the topic discussed in all the textbooks related to digital logic and system design might it be CMOS, TTL or any other logic family.

Let us illustrate the concept of noise margins with the help of an example. Let us assume that a signal has to travel from a transmitter to a receiver through an inter-connect element (or, commonly called as a net) which will only degrade the signal, since there is no active element in-between transmitter and receiver. The output signal produced by Transmitter (Tx) will deviate from ideal voltage levels as is shown in figures 1 and 2 for logic level ‘1’. In addition, there will be signal degradation by inter-connect element as well as noise induced from the surroundings. As a result, the band of voltages that can be present at the receiver input for logic ‘1’ will further widen. Now, there are two cases:

1. If the band voltages recognized as logic ‘1’ by the receiver is super-set of the band of voltages that can exist at the receiver input as shown in figure 1, receiver will recognize the transmitted logic ‘1’ for all the cases. This is the desired scenario as no logic ‘1’ transmitted will be missed by the receiver. This scenario is depicted in figure 1, wherein the noise induced by surroundings is such that the range of voltages present at the receiver does not violate the band of voltages recognized as voltage '1' by the receiver. So, it will be recognized correctly as logic '1' by the receiver.

Figure 1: Figure showing the noise induced is less than noise margin

2)  If the band of values recognized as logic ‘1’ by the receiver is a sub-set of the band of voltages that can exist at the receiver input as shown in figure 2, there will be some cases that will not be recognized as logic ‘1’, but are intended to be recognized. So, there will be a loss of information/incorrect transmission of information possible in such cases. This scenario is depicted in figure 2, wherein the noise induced by surroundings makes the band of voltage at the receiver's input larger than that can be decoded correctly as logic '1' by the receiver. So, there is no guarantee that the signal will be perceived as logic '1' by the receiver.

Figure 2: Figure showing the noise induced is greater than noise margin

Let us now label each of these regions to make the discussion more meaningful. The lowest voltage that will be produced as logic ‘1’ by the transmitter is termed as VOH and, let us say, highest is VDD. (We are here considered about lower level only). So, the range of voltages produced by the transmitter is (VDD – VOH).  And let the receiver accept voltages higher than VIH. So the range of voltages accepted by the receiver will be (VDD – VIH). So, the maximum degradation that can happen over the communication channel is (VOH – VIH) which is nothing but the noise margin. If the degradation is less than this figure, the logic ‘1’ will be recognized correctly by the receiver; otherwise it won’t. So, the noise margin equation can be given as below for logic '1':

Noise margin for logic '1' (NM) = VOH – VIH

Where

VOH = Lowest level of voltage that can be produced as logic '1' by the transmitter

VIH = Lowest level of voltage that can be recognized as logic '1' by the receiver

Similarly, for logic ‘0’, the range of outputs that can be produced by the transmitter is (0 - VOL) and the range of input voltages that can be detected by the receiver is (0 – VIL), thereby providing the noise margin as:

Noise margin (NM) = VIL – VOL

Where

VIL = Highest level of voltage that can be recognized as logic ‘0’ by the receiver.

VIH = Highest level of voltage that is produced as logic ‘0’ by the transmitter.

Figure 3 shows all these levels for the example we had taken earlier to demonstrate the concept of noise margins.

Figure 3: Noise margin

From out preceding discussion, if the degradation over the communication channel is more than noise margin, it will not be detected correctly by the receiver. So, it is imperative for the designer to design accordingly.

Definition of noise margin: Thus, we can conclude this post by defining noise margin as below:

"Noise margin is the difference between the worst signal voltage produced by the transmitter and the worst signal that can be detected by receiver."

Also read: 

• Latchup in CMOS devices
• Metal ECO - the process
• Regions of operation of MOS transistors
• False paths - what are they
• Latency and throughput - the two measures of system performance

Can a net have negative propagation delay?

As we discussed in ‘’Is it possible for a logic gate to have negative propagation delay”, a logic cell can have negative propagation delay. However, the only condition we mentioned was that the transition at the output pin should be improved drastically so that 50% level at output is reached before 50% level of input waveform.

In other words, the only condition for negative delay is to have improvement in slew. As we know, a net has only passive parasitic in the form of parasitic resistances and capacitances. Passive elements can only degrade the transition as they cannot provide energy (assuming no crosstalk); rather can only dissipate it. In other words, it is not possible for a net to have negative propagation delay.

However, we can have negative delay for a net, if there is crosstalk, as crosstalk can improve the transition on a net. In other words, in the presence of crosstalk, we can have 50% level at output reached before 50% level at input; hence, negative propagation delay of a net.

Also read:

• Bubble errors and bubble error correction
• Noise margins
• Can hold be frequency dependant
• Worst slew propagation
• Latchup in CMOS devices

Can hold check be frequency dependant?

We often encounter people argue that hold check is frequency independent. However, it is only partially true. This condition is true only for zero-cycle hold checks. By zero cycle hold checks, we mean that the hold check is performed on the same edge at which it is launched. This is true in case of timing paths between same polarity registers; e.g. between positive edge-triggered flops. Figure 1 below shows timing checks for a data-path launched from a positive edge-triggered flip-flop and captured at a positive edge-triggered flip-flop. The hold timing, in this case, is checked at the same edge at which data is launched. Changing the clock frequency will not cause hold check to change.

Figure 1: Setup and hold checks for positive edge-triggered to positive edge-triggered flip-flop

Most of the cases in today’s designs are of this type only. The exceptions to zero cycle hold check are not too many. There are hold checks for previous edge also. However, these are very relaxed as compared to zero cycle hold check. Hence, are not mentioned. Also, hold checks on next edge are impossible to be met considering cross-corner delay variations. So, seldom do we hear that hold check is frequency dependant. Let us talk of different scenarios of frequency dependant hold checks:

1.  From positive edge-triggered flip-flop to negative edge-triggered flip-flop and vice-versa: Figure 2 below shows the setup and hold checks for a timing path from positive edge-triggered flip-flop to a negative edge-triggered flip-flop. Change in frequency will change the distance between the two adjacent edges; hence, hold check will change. The equation for hold timing will be given for below case as:

T_data + T_clk/2 > T_skew + T_hold

or

Tslack =  T_clk/2 - T_hold - T_skew + T_data

          Thus, clock period comes into picture in calculation of hold timing slack.

Figure 2: Setup and hold checks for timing path from positive edge-triggered flip-flop to negative edge-triggered flip-flop

Similarly, for timing paths launching from negative edge-triggered flip-flop and being captured at positive edge-triggered flip-flop, clock period comes into picture. However, this check is very relaxed most of the times. It is evident from above equation that for hold slack to be negative, the skew between launch and capture clocks should be greater than half clock cycle which is very rare scenario to occur. Even at 2 GHz frequency (T_clk = 500 ps), skew has to be greater than 250 ps which is still very rare.

Coming to latches, hold check from a positive level-sensitive latch to negative edge-triggered flip-flop is half cycle. Similarly, hold check from a negative level-sensitive latch to positive edge-triggered flip-flop is half cycle. Hence, hold check in both of these cases is frequency dependant.

2. Clock gating hold checks: When data launched from a negative edge-triggered flip-flop gates a clock on an OR gate, hold is checked on next positive edge to the edge at which data is launched as shown in figure 3, which is frequency dependant.

Figure 3: Clock gating hold check between data launched from a negative edge-triggered flip-flop and and clock at an OR gate

           Similarly, data launched from positive edge-triggered and gating clock on an AND gate form half cycle hold. However, this kind of check is not possible to meet under normal scenarios considering cross-corner variations.

3)      Non-default hold checks: Sometimes, due to architectural requirements (e.g. multi-cycle paths for hold), hold check is non-zero cycle even for positive edge-triggered to positive edge-triggered paths as shown in figure 4 below.

Figure 4: Non-default hold check with multi-cycle path of 1 cycle specified

Also read:

• Lockup latch - principle, application and timing
• Data checks - all about data setup and data hold checks
• Worst slew propagation
• On-chip variations - the STA takeaway

Multicycle paths : The architectural perspective

Definition of multicycle paths: By definition, a multi-cycle path is one in which data launched from one flop is allowed (through architecture definition) to take more than one clock cycle to reach to the destination flop. And it is architecturally ensured either by gating the data or clock from reaching the destination flops. There can be many such scenarios inside a System on Chip where we can apply multi-cycle paths as discussed later. In this post, we discuss architectural aspects of multicycle paths. For timing aspects like application, analysis etc, please refer Multicycle paths handling in STA.

Why multi-cycle paths are introduced in designs: A typical System on Chip consists of many components working in tandem. Each of these works on different frequencies depending upon performance and other requirements. Ideally, the designer would want the maximum throughput possible from each component in design with paying proper respect to power, timing and area constraints. The designer may think to introduce multi-cycle paths in the design in one of the following scenarios:

      

       1)      Very large data-path limiting the frequency of entire component: Let us take a hypothetical case in which one of the components is to be designed to work at 500 MHz; however, one of the data-paths is too large to work at this frequency. Let us say, minimum the data-path under consideration can take is 3 ns. Thus, if we assume all the paths as single cycle, the component cannot work at more than 333 MHz; however, if we ignore this path, the rest of the design can attain 500 MHz without much difficulty. Thus, we can sacrifice this path only so that the rest of the component will work at 500 MHz. In that case, we can make that particular path as a multi-cycle path so that it will work at 250 MHz sacrificing the performance for that one path only.

     

     2)      Paths starting from slow clock and ending at fast clock: For simplicity, let us suppose there is a data-path involving one start-point and one end point with the start-point receiving clock that is half in frequency to that of the end point. Now, the start-point can only send the data at half the rate than the end point can receive. Therefore, there is no gain in running the end-point at double the clock frequency. Also, since, the data is launched once only two cycles, we can modify the architecture such that the data is received after a gap of one cycle. In other words, instead of single cycle data-path, we can afford a two cycle data-path in such a case. This will actually save power as the data-path now has two cycles to traverse to the endpoint. So, less drive strength cells with less area and power can be used. Also, if the multi-cycle has been implemented through clock enable (discussed later), clock power will also be saved.

Implementation of multi-cycle paths in architecture: Let us discuss some of the ways of introducing multi-cycle paths in the design:

      1)      Through gating in data-path: Refer to figure 1 below, wherein ‘Enable’ signal gates the data-path towards the capturing flip-flop. Now, by controlling the waveform at enable signal, we can make the signal multi-cycle. As is shown in the waveform, if the enable signal toggles once every three cycles, the data at the end-point toggles after three cycles. Hence, the data launched at edge ‘1’ can arrive at capturing flop only at edge ‘4’. Thus, we can have a multi-cycle of 3 in this case getting a total of 3 cycles for data to traverse to capture flop. Thus, in this case, the setup check is of 3 cycles and hold check is 0 cycle.

Figure 1: Introducing multicycle paths in design by gating data path

    Now let us extend this discussion to the case wherein the launch clock is half in frequency to the capture clock. Let us say, Enable changes once every two cycles. Here, the intention is to make the data-path a multi-cycle of 2 relative to faster clock (capture clock here). As is evident from the figure below, it is important to have Enable signal take proper waveform as on the waveform on right hand side of figure 2. In this case, the setup check will be two cycles of capture clock and hold check will be 0 cycle.

   

   

Figure 2: Introducing multi-cycle path where launch clock is half in  frequency to capture clock

        2) Through gating in clock path: Similarly, we can make the capturing flop capture data once every few cycles by clipping the clock. In other words, send only those pulses of clock to the capturing flip-flop at which you want the data to be captured. This can be done similar to data-path masking as discussed in point 1 with the only difference being that the enable will be masking the clock signal going to the capturing flop. This kind of gating is more advantageous in terms of power saving. Since, the capturing flip-flop does not get clock signal, so we save some power too.

    

Figure 3: Introducing multi cycle paths through gating the clock path

      Figure 3 above shows how multicycle paths can be achieved with the help of clock gating. The enable signal, in this case, launches from negative edge-triggered register due to architectural reasons (read here). With the enable waveform as shown in figure 3, flop will get clock pulse once in every four cycles. Thus, we can have a multicycle path of 4 cycles from launch to capture. The setup check and hold check, in this case, is also shown in figure 3. The setup check will be a 4 cycle check, whereas hold check will be a zero cycle check.

Pipelining v/s introducing multi-cycle paths: Making a long data-path to get to destination in two cycles can alternatively be implemented through pipelining the logic. This is much simpler approach in most of the cases than making the path multi-cycle. Pipelining means splitting the data-path into two halves and putting a flop between them, essentially making the data-path two cycles. This approach also eases the timing at the cost of performance of the data-path. However, looking at the whole component level, we can afford to run the whole component at higher frequency. But in some situations, it is not economical to insert pipelined flops as there may not be suitable points available. In such a scenario, we have to go with the approach of making the path multi-cycle.

References:

• Basics of multicycle and false paths - EDN.com

Setup checks and hold checks for flop-to-flop paths

In the post (Setup time and hold time – static timing analysis), we introduced setup and hold timing requirements and also discussed why these requirements exist. In this post, we will be discussing how these checks are applied for different cases for paths starting from and ending at flip-flops.

In present day designs, most of the paths (more than 95%) start from and end at flip-flops (exceptions are there like paths starting from and/or ending at latches). There can be flops which are positive edge triggered or negative edge triggered. Thus, depending upon the type of launching flip-flop and capturing flip-flop, there can be 4 cases as discussed below:

1)      Setup and hold checks for paths launching from positive edge-triggered flip-flop and being captured at positive edge-triggered flip-flop (rise-to-rise checks): Figure 1 shows a path being launched from a positive edge-triggered flop and being captured on a positive edge-triggered flop. In this case, setup check is on the next rising edge and hold check is on the same edge corresponding to the clock edge on which launching flop is launching the data.

Figure 1 : Timing path from positive edge flop to positive edge flop (rise to rise path)

Figure 2 below shows the setup and hold checks for positive edge-triggered register to positive edge-triggered register in the form of waveform. As is shown, setup check occurs at the next rising edge and hold check occurs at the same edge corresponding to the launch clock edge. For this case setup timing equation cab be given as:

            T_ck->q + T_prop + T_setup < T_period + T_{skew               (for setup check)}
And the equation for hold timing can be given as:

            T_ck->q + T_prop > T_hold + T_{skew                                  (for hold check)}

Where

        T_ck->q  : Clock-to-output delay of launch register

        T_prop : Maximum delay of the combinational path between launch and capture register

       T_hold : Hold time requirement of capturing register

       T_skew : skew between the two registers (Clock arrival at capture register - Clock arrival at launch register)

 

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window
                Start of data valid window = T_launch + T_hold
                End of data valid window = T_launch + T_period – T_setup

In other words, data at the input of capture register can toggle any time between (T_launch + T_hold) and (T_launch + T_period – T_setup).

Figure 3: Figure showing data valid window for rise-to-rise path

2)        Setup and hold checks for paths launching from positive edge-triggered flip-flop and being captured at negative edge-triggered flip-flop: In this case, both setup and hold check are half cycle checks; setup being checked on the next falling edge at the capture flop and hold on the previous falling edge of clock at the capture flop (data is launched at rising edge). Thus, with respect to (case 1) above, setup check has become tight and hold check has relaxed.

Figure 4: Timing path from positive edge flop to negative edge flop (Rise-to-fall path)

Figure 5 below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next falling edge and hold check occurs at the previous falling edge corresponding to the launch clock edge. The equation for setup check can be written, in this case, as:

            T_ck->q + T_prop + T_setup  < (T_period/2) + T_{skew                       (for setup check)}

And the equation for hold check can be written as:
            T_ck->q + T_prop + (T_period/2) > T_hold + T_{skew                         (for hold check)}

 

Figure 5: Setup and hold checks for rise-to-fall paths

Also, we show below the data valid and invalid windows. From this figure, 

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch – (T_period/2)+ T_hold

                End of data valid window = T_launch + (T_period/2) – T_setup

As we can see, the data valid window is spread evenly on both sides of launch clock edge.

 

Figure 6: Figure showing data valid window for rise-to-fall path

3)           Setup and hold checks for paths launching from negative edge-triggered flip-flop and being captured at positive edge-triggered flip-flop (rise-to-fall paths): This case is similar to case 2; i.e. both setup and hold checks are half cycle checks. Data is launched on negative edge of the clock, setup is checked on the next rising edge and hold on previous rising edge of the clock.

Figure 7: Timing path from negative edge flop to positive edge flop (fall-to-rise path)

Figure 8 below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next rising edge and hold check occurs at the previous rising edge corresponding to the launch clock edge.  The equation for setup check can be written, in this case, as:

            T_ck->q + T_prop + T_setup  < (T_period/2) + T_{skew                       (for setup check)}

And the equation for hold check can be written as:
            T_ck->q + T_prop + (T_period/2) > T_hold + T_{skew                         (for hold check)}

Figure 8: Setup and hold checks for fall to rise paths

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch – (T_period/2)+ T_hold

                End of data valid window = T_launch + (T_period/2) – T_setup

In this case too, data valid window spreads evenly on both the sides of launch clock edge.

 

Figure 9: Figure showing data valid window for fall-to-rise path

4)             Setup and hold checks for paths launching from negative edge-triggered flip-flop and being captured at negative edge-triggered flip-flop (fall-to-fall paths): The interpretation of this case is similar to case 1. Both launch and capture of data happen at negative edge of the clock. Figure 10 shows a path being launched from a negative edge-triggered flop and being captured on a negative edge-triggered flop. In this case, setup check is on the next falling edge and hold check is on the same edge corresponding to the clock edge on which launching flop is launching the data.

Figure 10: Path from negative edge flop to negative edge flop (fall to fall path)

Figure below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next falling edge and hold check occurs at the same edge corresponding to the launch clock edge. 
The equation for setup check can be given as:

                T_ck->q + T_prop + T_setup < T_period + T_{skew                (for setup check)
And the equation for hold check can be given as:}

               T_ck->q + T_prop > T_hold + T_{skew                                                    (for hold check)} 

Figure 11: Setup and hold check for fall-to-fall path

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch + T_hold

                End of data valid window = T_launch + T_period – T_setup

 

Figure 12: Figure showing data valid window for fall-to-fall path

Related posts:

• Setup time and hold time : static timing analysis
• Setup and hold checks for latch-to-reg and reg-to-latch paths
• Data checks: data setup and data hold checks
• On-chip variations
• Race conditions