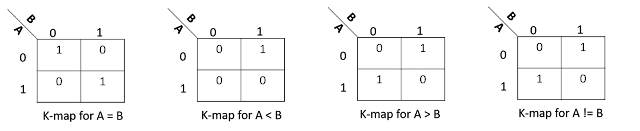
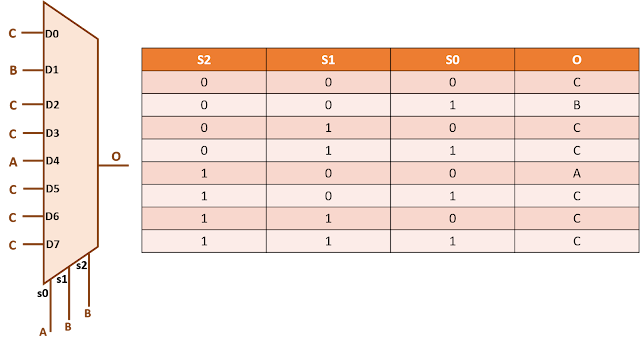
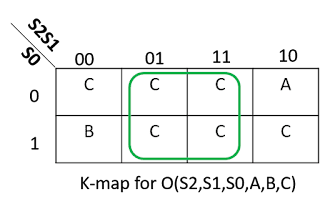
Priority multiplexer

Priority multiplexers are common in case one of the inputs is to be prioritized. The reason for this can be either functional or timing. In case of timing being the reason, the most setup timing critical input is connected to the highest priority input. The reason is that the highest priority signal gets the least logic in its path in a priority multiplexer as discussed below. The schematic for a 4-input priority mux is shown in figure 1 below:

In the above diagram, X0 has the highest priority; followed by X1, X2 and X3. A priority multiplexer selects the input if the corresponding select line is "1" and none of the select lines with with higher priority is "1". For example, if S0 is "1", X0 will be selected always. But if S2 is "1", X2 will be selected only if both S1 and S0 are "0".

The logic equation of a priority mux can be written as:

Y = S0.X0 + S0'.S1.X1 + S0'.S1'.S2 X2 + S0'.S1'.S2'.S3.X3 + S0'.S1'.S2'.S3'.S4.X4 + ......

Or, for a 4-input priority mux,

Y = S0.X0 + S0'.S1.X1 + S0'.S1'.S2 X2 + S0'.S1'.S2'.S3.X3

The output of the priority mux is not valid if all the select signals are "0", as we dont know which input to select in that case. That is why, figure 1 shows the D0 of the left multixer as don't care.

How a priority mux differs from a normal mux: In a normal mux, all the inputs have equal priorities, whereas they have different priorities in case of a priority mux.

Design problem: Design a circuit that delays the positive edge of a signal by one cycle

Here, we are given a problem wherein only ( 0 -> 1 ) transition of the signal is delayed by a single clock cycle whereas the other transition changes the output combination-ally. In other words, we are given the task to implement a Mealy state machine as output is both a function of state variables and input. However, this is a pretty simple problem involving single state. The output is a function of:

• Present input
• Input value one cycle before

Output should go "0" as soon as input goes "0". But it should go "1" when input one cycle back is "1". But there is a twist. What if current input is "0" and one cycle back, it was "1"? There is no clarity in the problem statement. Let us assume the output remains unchanged in such condition. The state transition table looks as shown below:

We can use K-map to solve for O. The solution is given in the figure below:

The resulting circuit is as shown in figure below.

Can you figure out the circuit that design that delays the negative edge of a signal by one cycle?

Design problem: How do you detect if two 8-bit numbers/signals are equal

Here, the problem involves detecting if each bit of a signal is equal to corresponding bit of the other signal and then generating a resultant. First of all, the circuit which provides equivalence of 1-bit is nothing but an XNOR gate as explained here. So, we require 8 XNOR gates to judge equivalence of individual bits. Even if one of the bits is "0", it means the numbers are not equal, which can be obtained by ANDing the eight bits together.

Alternatively, we can use an XOR gate as well. An XOR gate provides output as "1" if the two inputs are not equal as explained here. Even if one of the 8 individual XOR gates provides output as "1", it will mean that the numbers are not equal, which can be obtained by NORing the eight bits together.

Can you judge which of these can be implemented with less area and power?

Single-bit magnitude comparator

A single-bit magnitude comparator compares between two single-bit values. There can be 4 possible cases for two single bit values A and B as follows:

• A = B
• A > B
• A < B
• A != B

The truth table showing each of the cases is shown in figure below:

Let us use K-maps for deriving the logic for each of the four outputs as shown in figure below.

Thus, we get

Equation of (A = B) : A (xnor) B

Equation of (A < B) : A' B

 Equation of (A > B) : A B'

Equation of (A != B) : A (xor) B 

 

STA query : How positive edge trigger reg to positive latch path is zero cycle. But positive latch to rising flop is full cycle?

Ever thought why it is expected for setup checks to be single cycle or zero cycle? Common sense prevails that the data launched at any instant is expected to be captured at the next available instant, forming a setup check. We will explain here with the help of an example of latch-to-reg and reg-to-latch path.

Why setup check for postive latch to positive edge-triggered register is full cycle: Figure 1 below shows the clock waveforms for a positive latch to positive edge-triggered flip-flop timing paths. Positive edge-triggered register samples data only on positive edges. In the below figure, those instances are either "Time = 0" or "Time = T". The output of latch can change anytime when it is transparent. The earliest it can change is at "Time = 0+". So, the next instant it can get captured at the register is "Time = T". This makes the default setup check for such paths. That is why setup check for positive latch to positive edge-triggered registers is full cycle.

Figure 1: Single cycle setup check from positive latch to positive edge-triggered flip-flop

Why setup check for positive edge-triggered register to positive level-sensitive latch: Similar to the above case, figure 2 shows the clock wave-forms for positive edge-triggered flip-flop to positive latch timing paths. The flip-flop can launch data at either "Time = 0" or "Time = T". So, data will be available at its output at either "Time = 0+" or "Time = T+". The latch can capture the data at the same instant as it launched as it is transparent at that time. So, setup check is considered to be zero cycle in this case.

Figure 2: Zero cycle setup check from positive edge-triggered flip-flop to positive latch

We need to note that the "from" and "to" edges in these checks denoted in text-books (or shown in timing reports by STA tools by default) are default setup and hold checks. The actual setup and hold check edges are what is represented by the state machine the timing path belongs to. It is possible to ovverride default check edges by command set_multicycle_path. I would recommend going through setup and hold - the state machine essenstials to have a deeper understanding of this concept. In other words, you could have made positive latch to positive edge-triggered flip-flop setup check as single cycle. But you would also have to modify the hold check in that case. Can you guess what it would be?

Design problem: Logic minimization and restructuring for timing critical paths

Problem statement: An 8:1 multiplexer selects one out of three inputs based upon different combinations of S2, S1 and S0 as shown in figure below. Minimize the logic with a view that B is the most timing critical input.

Solution:

A 4-input MUX has one 4-input AND and one 8-input OR between each input and the output. However, since, there is one signal connected to many of the inputs, there seems to be a scope of logic minimization. Let us use K-map to minimize the logic for problem. The K-map for this problem is as shown below:

Writing the boolean expression, we get:

O = S2'S1'S0' C + S2'S1'S0 B + S1 C + S2S1'S0'A + S2S1'S0 C

O = C (S1 + S1' (S2  ⊕  S0)) + S2'S1'S0 B + S2 S1' S0' A

O = C (S1 + ( S2  ⊕  S0 )) + S2'S1'S0 B + S2 S1' S0' A   [Using A + A'B = A + B]

If we analyze carefully, we see that O is obtained by OR-ing three terms; one for A, one for B and one for C. The resulting structure is shown below:

Since, B is the most timing-critical input; there should be minimum logic between B and output. In other words, it should be closest to output. In the above figure, we see that there is a 4-input AND gate and a 3-input OR gate between O and B. We can reduce the logic between B and O by breaking 3-input OR into 2-input OR gates such that B is closest to output. similarly, we can break the 4-input AND gate into 2-input and 3-input AND gates. Thus, we are left with one 2-input AND gate and one 2-input OR gate between B and O as shown in figure below.

We see that there is still a possibility of logic re-structuring between B and O. De-Morgans theorem states that 

A + B = (A' B')'

Going by this, we can convert the OR gate at the output into NAND gate as shown in figure below.

The bubbles at the input of NAND gate can be moved to the outputs of respective drivers. Or, saying, more sophistically, there are two NAND gates between B and O.

Thus, we have achieved our purpose of

• Minimizing the logic
• Assuring that there is minimum logic between B and O, since B is the most timing critical input.

We need to keep in mind that there may be more than one solutions to each logic minimization problems. Can you think of a better realization of the circuit in question? What could have been the realization of the circuit in case C was the most timing critical input?