Programming problem: Synthsizable filter design in C++

Problem statement: Develop a synthesizable C/C++ function which is capable of performing image filtering. The filtering operation is defined by following equation:

// B -> filtered image

// A -> Input image

// h -> filter coefficients

int filter_func() {

                const int L = 1;

                const int x_size = 255;

                const int y_size = 255;

                int A_image[x_size][y_size];

                int B_image[x_size][y_size];

                int h[2*L+1][2*L+1];

                // Initializing the filtered image

                for (int i = 0; i < x_size; i++) {

                                for (int j = 0; j < y_size; j++) {

                                                B_image[i][j] = 0;

                                }

                }

                for (int i = 0; i < x_size; i++) {

                                for (int j = 0; j < y_size; j++) {

                                                for (int l = -L; l <= L; l++) {

                                                                for (int k = -L; k <= L; k++) {

                                                                                B_image[i][j] = B_image[i][j] + A_image[i-k][j-l]*h[k+L][l+L];

                                                                }

                                                }

                                }

                }

}

Hope you’ve found this post useful. Let us know what you think in the comments.

STA problem: Checking for setup/hold violations in a timing path

Problem: Figure 1 below shows a timing path from positive edge-triggered register to a positive edge-triggered register. Can you figure out if there is any setup and/or hold violation in the following circuit?

Figure 1: A sample timing path

Solution:

To check if a timing path violates setup and/or hold, we need to check if they satisfy setup and hold equations. A violating timing path has a negative setup/hold slack value.

The above circuit has a positive clock skew of 1 ns (as capture flip-flop gets clock 1 ns later than launch flip-flop).

Let us first check for setup violation. As we know, for a full cycle register-to-register timing path, setup equation is given as:

T_ck->q + T_prop + T_setup - Tskew < T_period

Here,

T_ck->q = 2 ns,  T_prop (max value of combinational propagation delay) = 4 ns,  T_setup = 1 ns, T_period = 10 ns, Tskew = 1 ns

Now, T_ck->q + T_prop + T_setup  = 2 + 4 + 1 - 1 = 6 ns < T_period

So, the above circuit does not have a setup violation. The setup slack, in this case, will be given as:

SS = T_{period -} (T_ck->q + T_prop + T_setup - Tskew₎ 

SS = +4 ns 

Since, setup slack comes out to be positive, this path does not have a setup violation.


Now, let us check is there is a hold violation for this timing path. Hold timing equation is given as:

T_ck->q  + T_prop > T_hold + T_skew

Here,

T_ck->q  =  2 ns, T_prop (min value of combinational propagation delay) = 2 ns, T_hold = 2ns, T_skew = 1 ns

 Now, T_ck->q  + T_prop = 2 ns + 2 ns = 4 ns

And T_hold + T_skew = 2 ns + 1 ns = 3 ns

Now, 4 ns > 3 ns, so this circuit does not have a hold violation. The hold slack, in this case, will be given as:

HS = T_ck->q  + T_prop  - (T_hold + T_skew)  = +1 ns

Since, hold slack comes out to be positive, this path does not have a hold violation.

Also read:

• Finding the maximum frequency of operation of a timing path
• Setup and hold interview questions

Mice and poisonous bottles

Problem: There are 20 bottles filled with water, out of which exactly one is poisonous. We have to figure out the poisonous one. We have, with us, available some mice. When a mice tastes water from a bottle, it dies after exactly half an hour. We have one hour to figure out the poisonous bottle. What approach we should take.                                (Problem source : www.quora.com)

Solution: Each bottle can either be drunk from by a mice or not; i.e., there are two possibilities. We can interpret this as a binary number system problem wherein '1' represents that the mice has drunk from a bottle and '0' represents it has not.

Now, let us approach with a very simple but un-optimized method. Let us have 20 mice, and assign 1 mice to each bottle (1 mice will dring water from a bottle). After half an hour, one of the mice will die. Clearly, we have the culprit bottle. This solution requires 20 mice. But, we can have a better solution as discussed below. Another option can be to choose 1 mouse only. Let it drink from one bottle, wait for half an hour if it dies. If not, let it drink from next bottle. The maximum this approach can take is 10 hours, which is way more than the budget allocated. So, solution 2 is not for this problem.

To represent number 20, we need 5 binary digits. Let us number each bottle with numbers from 1 to 20 and assign binary code representing that number to the bottle. Now, each of the bottles has a unique 5 bit code. We can assume each bit representative of 1 mouse, '1' shows that the mouse will drink water from this bottle, '0' shows otherwise. 

Let us take an example. Bottle '12' will have code '01100', meaning that mouse 2 and 3 will drink water from it. The code for each bottle and respective interpretation is as shown below:

Bottle no	Code	Interpretation
1	"00000"	No mouse will drink water
2	"00001"	Mouse 1 will dring water
3	"00010"	Mouse 2 will drink water
4	"00011"	Mouse 1 and 2 will drink water
5	"00100"	Mouse 3 will drink water
6	"00101"	Mouse 1 and 3 will drink water
7	"00110"	Mouse 2 and 3 will drink water
8	"00111"	Mouse 1,2 and 3 will drink water
9	"01000"	Mouse 4 will drink water
10	"01001"	Mouse 1 and 4 will drink water
11	"01010"	Mouse 2 and 4 will drink water
12	"01011"	Mouse 1, 2 and 4 will drink water
13	"01100"	Mouse 3 and 4 will drink water
14	"01101"	Mouse 1, 3 and 4 will drink water
15	"01110"	Mouse 2, 3 and 4 will drink water
16	"01111"	Mouse 1, 2, 3 and 4 will drink water
17	"10000"	Mouse 5 will drink water
18	"10001"	Mouse 1 and 5 will drink water
19	"10010"	Mouse 2 and 5 will drink water
20	"10011"	Mouse 1, 2 and 5 will drink water

Let us say, bottle 15 had poison. So, after half an hour,  mouse 2, 3 and 4 will die as only these mice drank water from this bottle, with the help of which we will come to know that this bottle contained poison.

Implement 3-input gates using 2:1 muxes

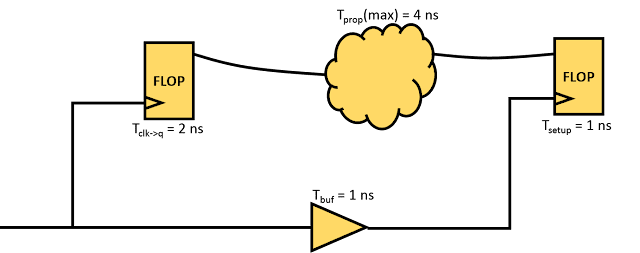
The implementation of 3-input gates using 2:1 muxes requires two stages of multiplexing logic as there is only 1 select line for a mux. Two of the variables can form as the select, one for each stage multiplexers. And the third input can act as the input of the first stage multiplexers depending upon the function needed. In this post, we will illustrate the process building a 3-input AND gate and a 3-input OR gate using 2:1 muxes:

3-input AND gate using 2:1 muxes: As we know, a AND gate's output goes '1' when all its inputs are '1', otherwise it is '0'. The truth table for a 3-input AND gate is shown below in figure 1, where A, B and C are the three inputs and O is the output.

                                      O = A (and) B (and) C

Truth table for 3-input AND gate

If we observe carefully, when A is 0, output is '0'. And when A is 1, output depends upon combination of B and C. So, we need at least two 2:1 muxes to implement 3-input AND gate. The mux closest to output can have A connected to the select, data0 input can be connected to '0'. data1 input needs to be connected to another mux that implements sub-function of B and C.

Now, if we observe the rows with A=1, when B = 0, O = 0. And when B = 1, O = C. So, to implement the sub-function, we need to connect B to select of mux, data0 of mux should be connected to '0' and data1 should be connected to 'C'.

Figure 2 below shows the implementation of 3-input AND gate using 2:1 muxes.

3-input AND gate using 2:1 muxes

3-input OR gate using 2:1 muxes: The output of an OR gate is '0' when all the inputs are '0', otherwise it is '1'. The truth table of a 3-input OR gate is shown in figure 3 below:

Truth table for 3-input OR gate

Looking at the truth table of 3-input OR gate, we see that when A = '1', output also goes '1'. And when A is '0', output is a sub-function of B and C. Seeing at the highlighted portion, when B = 0, output is equal to C. And when B is '1', output is also '1'.

Thus, we can connect the select of output side mux to A, with D0 input connected to another mux implementing sub-function of B and C and D1 input to '1'. The select of mux implementing sub-function can be connected to B, D0 to C and D1 to '1'.

Figure 4 below shows the implementation of 3-input OR gate using 2:1 muxes:

3-input OR gate using 2:1 muxes

3-input NAND gate using 2:1 mux: A NAND gate's output is 0 when all the inputs are 1. For all other combinations of inputs, the output is 1. The truth table for a 3-input NAND gate is shown in figure below. 

O = A (nand) B (nand) C

Truth table for 3-input NAND gate

Let us choose to have a 2:1 mux decoding the value of A. So, the mux closest to output will have its select connected to A. When A = 0, output is 1. So, pin D1 needs to be connected to "1". When A is 1, output is a further function of B and C. So, we need another mux. Let us choose to have B decode the value; i.e. B at the select of mux. When B = 0 & A = 1, O = 1. When B = 1 & A = 1, O = C'. The resulting logic using 2:1 muxes for a 3-input NAND gate is shown in figure below.

3-input NAND gate using 2:1 muxes

3-input NOR gate using 2:1 muxes: A 3-input NOR gate returns 0 when all the inputs are "0", otherwise the output is 1. The truth table for a 3-input NOR gate is shown in figure below.

Truth table for 3-input NOR Gate

Let us choose A to be the select of mux closest to output. When A is "1", output is "0". So, input-1 of the mux will be connected to logic "0". When A is "0", output is further a function of B and C.

Now, looking at the rows where A is "0", let us choose B to select the logic. When B is 1, output is "0" and when B is "0", output is invert of C. Thus, input-1 of this mux will be connected to "0" and other input to C'. Below figure shows the implementation of 3-input NOR gate using 2:1 muxes.

3-input NOR gate using 2:1 muxes

3-input XOR gate using 2:1 muxes: A 3-input XOR gate returns "1" when the odd number of inputs are "1". The truth table for 3-input XOR gate is shown in figure below.

Truth table for 3-input XOR gate

Let us choose A to be the select of mux closest to output. When A is "0", output is a function of B and C. So, we need another mux, let us choose B to be the select of this mux. Among the rows with A = 0, when B is "0", output is equal to C and when B is "1", output is equal to C'.

Similarly among the rows with A = "1", when B is "0", output is equal to C' and when B is "1", output is equal to C. The implementation of 3-input XOR gate using 2:1 muxes is shown in figure below.

3-input XOR gate using 2:1 muxes

3-input XNOR gate using 2:1 muxes: An XNOR gate returns "1" when even number of inputs are "1". Truth table of XNOR gate is shown in figure below.

Truth table of 3-input XNOR gate

Let us choose A to be the select of mux closest to output. When A is "0", output is a function of B and C. So, we need another mux, let us choose B to be the select of this mux. Among the rows with A = 0, when B is "0", output is equal to C' and when B is "1", output is equal to C.

Similarly among the rows with A = "1", when B is "0", output is equal to C and when B is "1", output is equal to C'. The implementation of 3-input XNOR gate using 2:1 muxes is shown in figure below.

3-iput XNOR gate using 2:1 muxes

Also read:

• XOR gate implementation using NAND gates
• 16x1 mux using 4x1 muxes
• 2-inputs gates using 2:1 mux

How to build an XOR gate using NAND gates

We can build a 2-input XOR gate using 5 NAND gates. Sound interesting, isn't it? Let us see how.

As we know, the logical equation of a 2-input XOR gate is given as below:

                      Y = A (xor) B = (A' B    +    A B')

Let us take an approach where we consider A and A' as different variables for now (optimizations related to this, if any, will consider later). Thus, the logic equation, now, becomes:

                       Y = (CB    +    A D)           -----   (i)

     where

                      C = A'     and      D = B'

De-Morgan's law states that

                                m + n = (m'n')'

Taking this into account,

                     Y = ((CB)'(AD)')' = ((A' B)'  (A B')')'

Thus, Y is equal to ((A' nand B) nand (A nand B')). No further optimizations to the logic seem possible to this logic. Figure 1 below shows the implementation of XOR gate using 2-input NAND gates.

Figure 1: 2-input XOR gate implementation using 2-input NAND gate

Thus, we have seen an XOR gate can be implemented by putting NAND gates in cascade. Can you think of a better way of implementing XOR gate using NAND gates?


Also read:

• XOR/XNOR gate using 2:1 mux
• Latch using 2:1 mux
• 2-input gates using 2:1 mux
• VHDL code for clock divider

STA problem: Maximum frequency of operation of a timing path

Problem: Figure 1 below shows a timing path from a positive edge-triggered register to a positive edge-triggered register. Can you figure out the maximum frequency of operation for this path?

Figure 1: A sample timing path

Solution:

The above timing path is a single cycle timing path. The maximum frequency is governed by setup timing equation. In other words, maximum frequency of operation is the maximum frequency (minimum time period of clock) that satisfies the following condition:

 T_ck->q + T_prop + T_setup - T_skew < T_period

Here,

 T_ck->q = 2 ns, T_prop = 4 ns, T_setup = 1 ns, T_skew = 1 ns, T_period 

Now,

T_period > 2 ns + 4 ns + 1 ns - 1 ns

T_period > 6 ns

So, the minimum time period of the clock required is 6 ns. And the maximum frequency that the above circuit can work is (1000/6) MHz = 166.67 MHz.

It should be noted that at if we operate this timing path at maximum frequency calculated, setup slack will be zero. :-)

In this post, we talked about frequency of operation of single cycle timing paths. Can you figure out maximum frequency of operation for half cycle timing paths? Also, there is a relation of maximum operating frequency to hold timing? Can you think about this situation?

Also read:

• Setup time and hold time basics
• Timing arcs
• What is Static Timing Analysis

Design Quiz: multiply by 2 clock circuit

Design problem: Make a simple circuit whose output clock is twice in frequency to the input clock.

An XOR gate with one of its input getting delayed version of the other input can act as a frequency multiplier. Since, an XOR gate produces a ‘0’ when both inputs are same, and ‘1’ when both inputs are different; if it gets delayed version of one input at the other, every time input toggles, a pulse is produced at the output. The duration of the pulse is equal to the delay introduced by delay element. The circuit and the resulting waveform is shown in figure 1 below. This circuit arrangement is also known as pulse generator as it produces a pulse on every toggle of input.

(a) Multiply-by-2 clock circuit                                      (b) Input and output clock waveforms of multiply-by-2                                                                                                 clock circuit

Characteristics of XOR multiply by 2:

• The output pulse duration is equal to the delay introduced by delay element.
• For duty cycle to be equal to 50%, the delay element’s delay must be half that of input clock. Since, this cannot be guaranteed, the output duty cycle will not be 50%.
• The delay element’s delay must be less than half the input clock period; otherwise it will not work
• The inactive state of XOR multiply-by-2 will be 0 as it produces a '0' when both inputs are same. To implement a multiply-by-2 circuit with '1' as inactive state, you will have to use an XNOR gate.

Hope you’ve found this post useful. Let us know what you think in the comments.

Also read:

• Designing a clock signal in VHDL
• Interesting design quiz - BCD multiply-by-5 circuit
• XOR/XNOR gate using 2:1 mux

Basics of latch timing

A latch is a digital logic circuit that can sample a 1-bit digital value and hold it depending upon the state of an enable signal. Based upon the state of enable, latches are categorized into positive level-sensitive and negative level-sensitive latches.

Positive level-sensitive latch: A positive level-sensitive latch follows the input data signal when enable is '1' and keeps its output when the data when it is '0'. Figure 1 below shows the symbol and the timing waveforms for a latch. As can be seen, whenever enable is '1', out follows the data input. And when enable in '0', out remains the same.

Figure 1(a): Positive level-                                             Figure 1(b): Timing waveform for a positive level-               sensitive latch                                                                                 sensitive latch                                        

Negative level-sensitive latch: A negative level-sensitive latch follows the input data when enable is '0' and keeps its output when input is '1'.

Figure 2(a): Negative level-                                             Figure 2(b): Timing waveform for a negative level-               sensitive latch                                                                                 sensitive latch                                      

Latch timing arcs: Data can propagate to the output of the latch in two ways as discussed below:

• Out changes with Data: This happens when enable is in its asserted state (for example, for a positive level latch). When this happens, Out follows Data as there is a direct path between Data and Out when Enable is '1'. This scenario is depicted in figures 1(b) and 2(b) above wherein out is shown toggling when Data toggles. The latch is, thus, said to have a timing arc from Data to Out.
• Out changes with Enable: This happens when Data at input changes when Enable is in its de-asserted state. When this happens, latch waits for Enable to be asserted, then, follows the value of Data. As figure 3 shows, Data had become stable a lot earlier, but out toggled only when enable became asserted. So, in latches, there exists a timing arc from Enable to Out.

Figure 3:When data changes during enable is in de-asserted state, output waits for the enable to assert. Only then, the effect of input propagated to output

• Relation between Data and Enable: If Data toggles very close to the closing edge of Enable, then, there might be a confusion as if its effect will be propagated to output or not (as discussed later in this post). To make things more deterministic, we impose a certain condition that Data should not toggle when Enable is getting de-asserted. This relationship can be modelled as setup and hold arcs. So, there are setup and hold timing arcs between data and enable pins of a latch. These will be discussed below in detail.

Setup time and hold time for a latch: The most commonly used latch circuit is that built using inverters and transmission gates. Figure 4 shows the transmission gate implementation of a positive level-sensitive latch. The Enable has been shown as CLK as usually is the case in sequential state machines. This circuit has two phases, as is expected for a latch:

• When CLK = '1', Transmission gate at the input gets ON and there is a direct path between Data and Out
• When CLK = '0', transmission gate in the loopback path gets ON. Out holds its value

Figure 4: Positive level-sensitive latch using transmission gates

Now, when CLK transitions from '1' to '0', it is important that Data does not toggle. The time before the clock falling edge that Data should remain stable is known as latch setup time. Similarly, the time after the clock falling edge that Data should remain stable is called latch hold time.

Let us go into the details of what latch setup and hold time should be for transmission gate latch. If we want the data to be propagated properly to the output, then Data should be stable for atleast some time before closing of the input transmission gate. This time is such that it goes into the memory of latch; i.e., before input transmission gate closes, Data should traverse both the inverters of the loop. So, setup time of the latch involves the delay of input transmission gate and the two inverters. Figure 5 below shows the setup time for the latch.

Figure 5: Setup time for latch

Similarly, if we do not want the data to propagate to output, it must not cross input transmission gate so that it does not disturb the present state of the latch. This server as the hold time for the latch. Assuming CLK' takes one inverter delay, input transmission gate will close after one inverter delay only. So, the hold time for Data is one inverter delay minus transmission gate delay. Please refer to figure 6 below for the illustration of this. (CLK)' is formed from CLK after a delay equivalent to an inverter delay. Only then, input transmission gate will switch off. If we want the data not to propagate to Out, we have to ensure that it does not cross input transmission gate. So, Data should not be present at the transmission gate's input at time (T(inv) - T(tg)). In other words, it has to be held stable this much time after CLK edge. This is the hold time for the latch.

Figure 6: Hold time for latch

Please note that there are other topologies also possible for latches such as dynamic latches etc. The setup time and hold time calculations for such topologies will vary, but the underlying principle will remain same, which is as follows:

• Setup time ensures that the data propagates to the output at the coming clock edge
• Hold time ensures that the data does not propagate to the output at the present/previous clock edge

Setup checks and hold checks for latches: As discussed above, the decision for the data to be latched or not to be latched is made at the closing edge. So, the setup and hold checks are with respect to latch closing edge only. However, since, latches are transparent during half of the clock period, we can assume as if the capturing edge is flexible and stretches all over the active level of the latch. This property enables a very beautiful concept known as "time borrowing" for latches.

Technology scaling factor

For instance, you will find technology nodes as 180 um 90 um, 65 um, 45 um, 32 um, 22 um and so on..

*Source - Digital integrated circuits - A design perspective by Jan M Rabay

Clock gating cell

Clock gating is a very common technique to save power by stopping the clock to a module when the module is not operating. As discussed in Clock switching and clock gating checks, there are two kinds of clock gating checks at combinational gates. We also discussed that for an AND type check, enable must launch from a negative edge-triggered flip-flop and for an OR type check, enable must launch from a positive edge-triggered flip-flop. However, it is very difficult to control the generic state machine to launch the signals to gate a clock either all from positive edge or from negative edge.

Evolution of integrated clock gating cell: To reduce the burden of same kind of launch registers from the state machine, an AND type clock gate can always be preceded with a negative level-sensitive latch and an OR type clock gate can be preceded with a positive level-sensitive latch. This has the same impact as a lockup latch in case of scan chain and eases hold timing. It results in zero cycle hold check from both positive and negative edge-triggered registers, without introduction of any additional latency. Since, each clock gate has to be preceded by a latch, why not build a special cell with an AND gate + a negative level-sensitive latch (or an OR gate + a positive level-sensitive latch). This concept served as motivation for Integrated Clock Gating Cell. This will provide more optimum area, power and timing for the resulting structure.

Test enable pin in integrated clock gating cell: During shift in scan testing, all the clock control signals have to be bypassed to let shifting happen. This can be achieved by providing a bypass signal called “test enable” that is ORed with functional enable signal (shown in figure 1 below). As soon as design goes into shift mode, test enable signal goes high, thereby bypassing all functional enable signals. So, it makes sense to embed this OR gate into integrated clock gating cell itself.

Structure of integrated clock gating cell: Figure 1 below shows the structure of the two kinds of integrated clock gating cells. The one on the left has an AND gate preceded by a negative level-sensitive latch. The enable and test_enable are active high. Clock_out has an inactive low state. The one on the right is complementary to this. It has an OR gate preceded by a positive level-sensitive latch. Both enable and test_enable are active high and output clock has an inactive high state. In case enable and test_enable are active low, NOR gate should be replaced by AND gate.

Figure 1: (a) AND type integrated clock gating cell                         Figure 1: (b) OR type integrated clock gating cell

Hope you’ve found this post useful. Let us know what you think in the comments.

Also read:

• Clock gating interview questions