LVS in VLSI

LVS stands for Layout vs Schematic. It is one of the steps of physical verification; the other one being DRC (Design Rule Check). While DRC only checks for certain layout rules to ensure the design will be manufactured reliably, functional correctness of the design is ensured by LVS.

Layout vs Schematic (LVS) compares the design layout with the design schematic/netlist to tell if the design is functionally equivalent to schematic. For this, the connections are extracted from layout of the design by using a set of rules to convert the layout to connections. These connections are, then compared if they match with the connections of the netlist. If the connections match, the LVS is said to be clean. 

Interesting problem – Latches in series

Problem: 100 latches (either all positive or all negative) are placed in series (figure 1). How many cycles of latency will it introduce?

Figure 1 : 100 negative level-sensitive latches in series

As we know, setup check between latches of same polarity (both positive or negative) is zero cycle with half cycle of time borrow allowed as shown in figure 2 below for negative level-sensitive latches:

Figure 2: Setup check between two negative level-sensitive latches

So, if there are a number of same polarity latches, all will form zero cycle setup check with the next latch; resulting in overall zero cycle phase shift.

As is shown in figure 3, all the latches in series are borrowing time, but allowing any actual phase shift to happen. If we have a design with all latches, there cannot be a next state calculation if all the latches are either positive level-sensitive or negative level-sensitive. In other words, for state-machine implementation, there should not be latches of same polarity in series.

Figure 3 : Timing for 100 latches in series

Hope you’ve found this post useful. Let us know what you think in the comments.

Also read:

• Build a latch using a 2:1 multiplexer
• Multicycle paths handling in STA
• Latchup in CMOS devices
• Lockup latch - principle, application and timing
• Data checks - all about data setup and data hold checks

Can a net have negative propagation delay?

As we discussed in ‘’Is it possible for a logic gate to have negative propagation delay”, a logic cell can have negative propagation delay. However, the only condition we mentioned was that the transition at the output pin should be improved drastically so that 50% level at output is reached before 50% level of input waveform.

In other words, the only condition for negative delay is to have improvement in slew. As we know, a net has only passive parasitic in the form of parasitic resistances and capacitances. Passive elements can only degrade the transition as they cannot provide energy (assuming no crosstalk); rather can only dissipate it. In other words, it is not possible for a net to have negative propagation delay.

However, we can have negative delay for a net, if there is crosstalk, as crosstalk can improve the transition on a net. In other words, in the presence of crosstalk, we can have 50% level at output reached before 50% level at input; hence, negative propagation delay of a net.

Also read:

• Bubble errors and bubble error correction
• Noise margins
• Can hold be frequency dependant
• Worst slew propagation
• Latchup in CMOS devices

On-chip variations – the STA takeaway

Static timing analysis of a design is performed to estimate its working frequency after the design has been fabricated. Nominal delays of the logic gates as per characterization are calculated and some pessimism is applied above that to see if there will be any setup and/or hold violation at the target frequency. However, all the transistors manufactured are not alike. Also, not all the transistors receive the same voltage and are at same temperature.  The characterized delay is just the delay of which there is maximum probability. The delay variation of a typical sample of transistors on silicon follows the curve as shown in figure 1. As is shown, most of the transistors have nominal characteristics. Typically, timing signoff is carried out with some margin. By doing this, the designer is trying to ensure that more number of transistors are covered. There is direct relationship between the margin and yield. Greater the margin taken, larger is the yield. However, after a certain point, there is not much increase in yield by increasing margins. In that case, it adds more cost to the designer than it saves by increase in yield. Therefore, margins should be applied so as to give maximum profits.

Number of transistors v/s delay for a typical silicon transistors sample

We have discussed above how variations in characteristics of transistors are taken care of in STA. These variations in transistors’ characteristics as fabricated on silicon are known as OCV (On-Chip Variations). The reason for OCV, as discussed above also, is that all transistors on-chip are not alike in geometry, in their surroundings, and position with respect to power supply. The variations are mainly caused by three factors:

• Process variations: The process of fabrication includes diffusion, drawing out of metal wires, gate drawing etc. The diffusion density is not uniform throughout wafer. Also, the width of metal wire is not constant. Let us say, the width is 1um +- 20 nm. So, the metal delays are bound to be within a range rather than a single value. Similarly, diffusion regions for all transistors will not have exactly same diffusion concentrations. So, all transistors are expected to have somewhat different characteristics.
• Voltage variation: Power is distributed to all transistors on the chip with the help of a power grid. The power grid has its own resistance and capacitance. So, there is voltage drop along the power grid. Those transistors situated close to power source (or those having lesser resistive paths from power source) receive larger voltage as compared to other transistors. That is why, there is variation seen across transistors for delay.
• Temperature variation: Similarly, all the transistors on the same chip cannot have same temperature. So, there are variations in characteristics due to variation in temperatures across the chip.

How to take care of OCV: To tackle OCV, the STA for the design is closed with some margins. There are various margining methodologies available. One of these is applying a flat margin over whole design. However, this is over pessimistic since some cells may be more prone to variations than others. Another approach is applying cell based margins based on silicon data as what cells are more prone to variations. There also exist methodologies based on different theories e.g. location based margins and statistically calculated margins. As advances are happening in STA, more accurate and faster discoveries are coming into existence.

Also read:

• Power aware RTL design
• Lockup latch - principle, application and timing
• Propagation delay of logic gates
• Defining a clock signal in VHDL

Multicycle paths : The architectural perspective

Definition of multicycle paths: By definition, a multi-cycle path is one in which data launched from one flop is allowed (through architecture definition) to take more than one clock cycle to reach to the destination flop. And it is architecturally ensured either by gating the data or clock from reaching the destination flops. There can be many such scenarios inside a System on Chip where we can apply multi-cycle paths as discussed later. In this post, we discuss architectural aspects of multicycle paths. For timing aspects like application, analysis etc, please refer Multicycle paths handling in STA.

Why multi-cycle paths are introduced in designs: A typical System on Chip consists of many components working in tandem. Each of these works on different frequencies depending upon performance and other requirements. Ideally, the designer would want the maximum throughput possible from each component in design with paying proper respect to power, timing and area constraints. The designer may think to introduce multi-cycle paths in the design in one of the following scenarios:

      

       1)      Very large data-path limiting the frequency of entire component: Let us take a hypothetical case in which one of the components is to be designed to work at 500 MHz; however, one of the data-paths is too large to work at this frequency. Let us say, minimum the data-path under consideration can take is 3 ns. Thus, if we assume all the paths as single cycle, the component cannot work at more than 333 MHz; however, if we ignore this path, the rest of the design can attain 500 MHz without much difficulty. Thus, we can sacrifice this path only so that the rest of the component will work at 500 MHz. In that case, we can make that particular path as a multi-cycle path so that it will work at 250 MHz sacrificing the performance for that one path only.

     

     2)      Paths starting from slow clock and ending at fast clock: For simplicity, let us suppose there is a data-path involving one start-point and one end point with the start-point receiving clock that is half in frequency to that of the end point. Now, the start-point can only send the data at half the rate than the end point can receive. Therefore, there is no gain in running the end-point at double the clock frequency. Also, since, the data is launched once only two cycles, we can modify the architecture such that the data is received after a gap of one cycle. In other words, instead of single cycle data-path, we can afford a two cycle data-path in such a case. This will actually save power as the data-path now has two cycles to traverse to the endpoint. So, less drive strength cells with less area and power can be used. Also, if the multi-cycle has been implemented through clock enable (discussed later), clock power will also be saved.

Implementation of multi-cycle paths in architecture: Let us discuss some of the ways of introducing multi-cycle paths in the design:

      1)      Through gating in data-path: Refer to figure 1 below, wherein ‘Enable’ signal gates the data-path towards the capturing flip-flop. Now, by controlling the waveform at enable signal, we can make the signal multi-cycle. As is shown in the waveform, if the enable signal toggles once every three cycles, the data at the end-point toggles after three cycles. Hence, the data launched at edge ‘1’ can arrive at capturing flop only at edge ‘4’. Thus, we can have a multi-cycle of 3 in this case getting a total of 3 cycles for data to traverse to capture flop. Thus, in this case, the setup check is of 3 cycles and hold check is 0 cycle.

Figure 1: Introducing multicycle paths in design by gating data path

    Now let us extend this discussion to the case wherein the launch clock is half in frequency to the capture clock. Let us say, Enable changes once every two cycles. Here, the intention is to make the data-path a multi-cycle of 2 relative to faster clock (capture clock here). As is evident from the figure below, it is important to have Enable signal take proper waveform as on the waveform on right hand side of figure 2. In this case, the setup check will be two cycles of capture clock and hold check will be 0 cycle.

   

   

Figure 2: Introducing multi-cycle path where launch clock is half in  frequency to capture clock

        2) Through gating in clock path: Similarly, we can make the capturing flop capture data once every few cycles by clipping the clock. In other words, send only those pulses of clock to the capturing flip-flop at which you want the data to be captured. This can be done similar to data-path masking as discussed in point 1 with the only difference being that the enable will be masking the clock signal going to the capturing flop. This kind of gating is more advantageous in terms of power saving. Since, the capturing flip-flop does not get clock signal, so we save some power too.

    

Figure 3: Introducing multi cycle paths through gating the clock path

      Figure 3 above shows how multicycle paths can be achieved with the help of clock gating. The enable signal, in this case, launches from negative edge-triggered register due to architectural reasons (read here). With the enable waveform as shown in figure 3, flop will get clock pulse once in every four cycles. Thus, we can have a multicycle path of 4 cycles from launch to capture. The setup check and hold check, in this case, is also shown in figure 3. The setup check will be a 4 cycle check, whereas hold check will be a zero cycle check.

Pipelining v/s introducing multi-cycle paths: Making a long data-path to get to destination in two cycles can alternatively be implemented through pipelining the logic. This is much simpler approach in most of the cases than making the path multi-cycle. Pipelining means splitting the data-path into two halves and putting a flop between them, essentially making the data-path two cycles. This approach also eases the timing at the cost of performance of the data-path. However, looking at the whole component level, we can afford to run the whole component at higher frequency. But in some situations, it is not economical to insert pipelined flops as there may not be suitable points available. In such a scenario, we have to go with the approach of making the path multi-cycle.

References:

• Basics of multicycle and false paths - EDN.com

Setup checks and hold checks for flop-to-flop paths

In the post (Setup time and hold time – static timing analysis), we introduced setup and hold timing requirements and also discussed why these requirements exist. In this post, we will be discussing how these checks are applied for different cases for paths starting from and ending at flip-flops.

In present day designs, most of the paths (more than 95%) start from and end at flip-flops (exceptions are there like paths starting from and/or ending at latches). There can be flops which are positive edge triggered or negative edge triggered. Thus, depending upon the type of launching flip-flop and capturing flip-flop, there can be 4 cases as discussed below:

1)      Setup and hold checks for paths launching from positive edge-triggered flip-flop and being captured at positive edge-triggered flip-flop (rise-to-rise checks): Figure 1 shows a path being launched from a positive edge-triggered flop and being captured on a positive edge-triggered flop. In this case, setup check is on the next rising edge and hold check is on the same edge corresponding to the clock edge on which launching flop is launching the data.

Figure 1 : Timing path from positive edge flop to positive edge flop (rise to rise path)

Figure 2 below shows the setup and hold checks for positive edge-triggered register to positive edge-triggered register in the form of waveform. As is shown, setup check occurs at the next rising edge and hold check occurs at the same edge corresponding to the launch clock edge. For this case setup timing equation cab be given as:

            T_ck->q + T_prop + T_setup < T_period + T_{skew               (for setup check)}
And the equation for hold timing can be given as:

            T_ck->q + T_prop > T_hold + T_{skew                                  (for hold check)}

Where

        T_ck->q  : Clock-to-output delay of launch register

        T_prop : Maximum delay of the combinational path between launch and capture register

       T_hold : Hold time requirement of capturing register

       T_skew : skew between the two registers (Clock arrival at capture register - Clock arrival at launch register)

 

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window
                Start of data valid window = T_launch + T_hold
                End of data valid window = T_launch + T_period – T_setup

In other words, data at the input of capture register can toggle any time between (T_launch + T_hold) and (T_launch + T_period – T_setup).

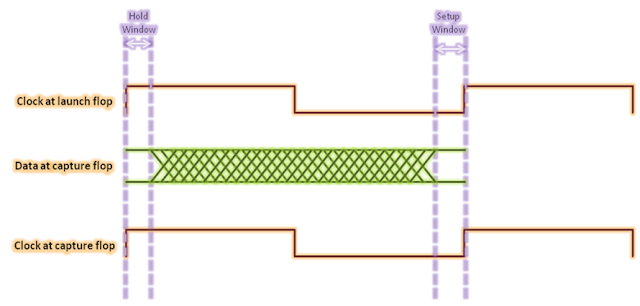Figure 3: Figure showing data valid window for rise-to-rise path

2)        Setup and hold checks for paths launching from positive edge-triggered flip-flop and being captured at negative edge-triggered flip-flop: In this case, both setup and hold check are half cycle checks; setup being checked on the next falling edge at the capture flop and hold on the previous falling edge of clock at the capture flop (data is launched at rising edge). Thus, with respect to (case 1) above, setup check has become tight and hold check has relaxed.

Figure 4: Timing path from positive edge flop to negative edge flop (Rise-to-fall path)

Figure 5 below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next falling edge and hold check occurs at the previous falling edge corresponding to the launch clock edge. The equation for setup check can be written, in this case, as:

            T_ck->q + T_prop + T_setup  < (T_period/2) + T_{skew                       (for setup check)}

And the equation for hold check can be written as:
            T_ck->q + T_prop + (T_period/2) > T_hold + T_{skew                         (for hold check)}

 

Figure 5: Setup and hold checks for rise-to-fall paths

Also, we show below the data valid and invalid windows. From this figure, 

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch – (T_period/2)+ T_hold

                End of data valid window = T_launch + (T_period/2) – T_setup

As we can see, the data valid window is spread evenly on both sides of launch clock edge.

 

Figure 6: Figure showing data valid window for rise-to-fall path

3)           Setup and hold checks for paths launching from negative edge-triggered flip-flop and being captured at positive edge-triggered flip-flop (rise-to-fall paths): This case is similar to case 2; i.e. both setup and hold checks are half cycle checks. Data is launched on negative edge of the clock, setup is checked on the next rising edge and hold on previous rising edge of the clock.

Figure 7: Timing path from negative edge flop to positive edge flop (fall-to-rise path)

Figure 8 below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next rising edge and hold check occurs at the previous rising edge corresponding to the launch clock edge.  The equation for setup check can be written, in this case, as:

            T_ck->q + T_prop + T_setup  < (T_period/2) + T_{skew                       (for setup check)}

And the equation for hold check can be written as:
            T_ck->q + T_prop + (T_period/2) > T_hold + T_{skew                         (for hold check)}

Figure 8: Setup and hold checks for fall to rise paths

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch – (T_period/2)+ T_hold

                End of data valid window = T_launch + (T_period/2) – T_setup

In this case too, data valid window spreads evenly on both the sides of launch clock edge.

 

Figure 9: Figure showing data valid window for fall-to-rise path

4)             Setup and hold checks for paths launching from negative edge-triggered flip-flop and being captured at negative edge-triggered flip-flop (fall-to-fall paths): The interpretation of this case is similar to case 1. Both launch and capture of data happen at negative edge of the clock. Figure 10 shows a path being launched from a negative edge-triggered flop and being captured on a negative edge-triggered flop. In this case, setup check is on the next falling edge and hold check is on the same edge corresponding to the clock edge on which launching flop is launching the data.

Figure 10: Path from negative edge flop to negative edge flop (fall to fall path)

Figure below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next falling edge and hold check occurs at the same edge corresponding to the launch clock edge. 
The equation for setup check can be given as:

                T_ck->q + T_prop + T_setup < T_period + T_{skew                (for setup check)
And the equation for hold check can be given as:}

               T_ck->q + T_prop > T_hold + T_{skew                                                    (for hold check)} 

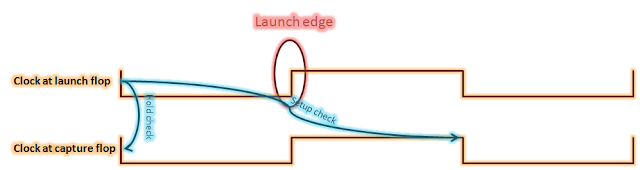Figure 11: Setup and hold check for fall-to-fall path

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch + T_hold

                End of data valid window = T_launch + T_period – T_setup

 

Figure 12: Figure showing data valid window for fall-to-fall path

Related posts:

• Setup time and hold time : static timing analysis
• Setup and hold checks for latch-to-reg and reg-to-latch paths
• Data checks: data setup and data hold checks
• On-chip variations
• Race conditions