Interesting programming quiz : Array Bound Read Error

Problem: Can you figure out what is wrong with following piece of code?

#include <iostream>int main() {     int a[5] = {1,2,3,4,5};     for (int i = 4; a[i] >= 0 && i >=0 ; i--) {          std::cout<< "ith element of array is "<<a[i]<<std::endl;     }}

I would suggest you to  try it yourself before scrolling down to see the answer. Its quite interesting,

......

......

......

......

......

......

......

......

......

......

......

......

......

......

......

......

......

......

Answer : Here, as one can figure out, the intention is to print array elements from end till we don't hit any negative number. In the first look it may seem fine but unfortunately it will end up in ABR (Array Bound Read).

Explanation : After the completion of 5th iteration; i.e. when i = 0, compiler will decrement i;  i.e., i will become "-1". It will, then, try to check the condition, which will result in reading a[-1]. Since, array can have indexes only greater than or equal to 0, it will result in an error. Trying to read array elements out of the allowed indexes is termed as Array Bound Read Error. Hence, one should avoid such conditions because it can result into random result. The program can crash anytime. If you are lucky, it may run successfully also. Its all up to your luck.  Instead, it should be

for (int i = 5; i>=0 && a[i]  >= 0 ; i--) {

i.e. first check index value and then do the array access operation.

Here, with the above solution, one more interesting thing comes up to understand. In AND (&&) operation compiler first evaluates  condition1; if it is true, then goes to evaluate condition2; otherwise return false from there only.

For example,

#include <iostream>
int main() {int i = 0;int j= 1;if(  ( i == 1) && (++j ==3)  ) {      std::cout<<"inside if"<<std::endl;}std::cout<<"i is "<<i<<" and j is "<<j<<std::endl;}

Output :

i is 0 and j is 1

Here, as you can see code control will not go into if branch as none of condition is true. since condition1 i==1 is false, compiler will not even check condition2 i.e. value of j will not be incremented.

Internally,  compiler might be doing some following kind of transformation to evaluate && operation

  bool cond = (i==1);  if( cond ) {      cond = (++j != 0) ;  }if(cond){      std::cout<<"inside if"<<std::endl;}

Also read:

• Automatic include of header dependencies in makefile
• Library
• C++ trivia
• Some good reads about process
• String class vs dynamically allocated array

Function Overloading

Function overloading is a feature inherent in many programming languages including c++. It allows a user to write multiple functions with same name but with different signatures. On calling the function, the version of the function corresponding to the signature will be referred to. Function signature includes function parameters/arguments, but it does not include return type. Function signature may differ in terms of number of parameters or type of parameters. Let us illustrate with the help of a few examples:

Example 1: The two functions below are overloaded, since the return type of arguments differ:

int func(int a,int b);double func(double a,double b);

Example 2: The two functions below are overloaded because they differ in the number of arguments:

int func(int a,int b);int func(int a,int b,int c);

Example 3: The two functions below are not overloaded because they differ only in terms of their return type; the number and type of all the arguments is same.

void func(int a,int b,int c);int func(int a,int b,int c);

Please note that C does not support function overloading because there is no concept of name mangling in C. On the other hand, C++ does support function overloading as name mangling is supported in C++. Name mangling is mangled name of function name and its signature which is used by C++ compiler internally to refer to functions. For instance, in above example 1, mangled name of functions will look something like shown below:

func__int_intfunc__double_double

This way C++ compiler can handle function overloading. 

Note : above are not the actual mangled names. Compiler can make some more complicated names. this is just for understanding. 

Also read:

• Meyer's singleton pattern
• Function overloading
• Comparison between array, linked list and vector
• C function for hexadecimal to decimal conversion
• Problem - can you figure out is there something wrong with this code

On-chip variations – the STA takeaway

Static timing analysis of a design is performed to estimate its working frequency after the design has been fabricated. Nominal delays of the logic gates as per characterization are calculated and some pessimism is applied above that to see if there will be any setup and/or hold violation at the target frequency. However, all the transistors manufactured are not alike. Also, not all the transistors receive the same voltage and are at same temperature.  The characterized delay is just the delay of which there is maximum probability. The delay variation of a typical sample of transistors on silicon follows the curve as shown in figure 1. As is shown, most of the transistors have nominal characteristics. Typically, timing signoff is carried out with some margin. By doing this, the designer is trying to ensure that more number of transistors are covered. There is direct relationship between the margin and yield. Greater the margin taken, larger is the yield. However, after a certain point, there is not much increase in yield by increasing margins. In that case, it adds more cost to the designer than it saves by increase in yield. Therefore, margins should be applied so as to give maximum profits.

Number of transistors v/s delay for a typical silicon transistors sample

We have discussed above how variations in characteristics of transistors are taken care of in STA. These variations in transistors’ characteristics as fabricated on silicon are known as OCV (On-Chip Variations). The reason for OCV, as discussed above also, is that all transistors on-chip are not alike in geometry, in their surroundings, and position with respect to power supply. The variations are mainly caused by three factors:

• Process variations: The process of fabrication includes diffusion, drawing out of metal wires, gate drawing etc. The diffusion density is not uniform throughout wafer. Also, the width of metal wire is not constant. Let us say, the width is 1um +- 20 nm. So, the metal delays are bound to be within a range rather than a single value. Similarly, diffusion regions for all transistors will not have exactly same diffusion concentrations. So, all transistors are expected to have somewhat different characteristics.
• Voltage variation: Power is distributed to all transistors on the chip with the help of a power grid. The power grid has its own resistance and capacitance. So, there is voltage drop along the power grid. Those transistors situated close to power source (or those having lesser resistive paths from power source) receive larger voltage as compared to other transistors. That is why, there is variation seen across transistors for delay.
• Temperature variation: Similarly, all the transistors on the same chip cannot have same temperature. So, there are variations in characteristics due to variation in temperatures across the chip.

How to take care of OCV: To tackle OCV, the STA for the design is closed with some margins. There are various margining methodologies available. One of these is applying a flat margin over whole design. However, this is over pessimistic since some cells may be more prone to variations than others. Another approach is applying cell based margins based on silicon data as what cells are more prone to variations. There also exist methodologies based on different theories e.g. location based margins and statistically calculated margins. As advances are happening in STA, more accurate and faster discoveries are coming into existence.

Also read:

• Power aware RTL design
• Lockup latch - principle, application and timing
• Propagation delay of logic gates
• Defining a clock signal in VHDL

Depletion MOSFET and negative logic. Why it is not possible?

As we know, depletion MOSFET conducts current even with gate and source at same voltage level. To cut-off the current in depletion MOSFET, a voltage has to be applied at gate so as to exhaust the already existing carriers inside the channel. On the other hand, enhancement type MOSFET is cut-off when gate and source are at same voltage.

Taking the example of NMOS, for a depletion MOS, with source and gate at same level, there is still a channel available, hence, it conducts electric current. To bring it to cut-off, a negative potential is needed to be applied at gate (considering source at ‘X’ potential). Thus, with source at ‘X’ potential and gate at ‘X’ potential, drain attains the potential of source. Since, to cut-off the device, gate has to be given a voltage less than ‘X’, so we can say “when Gate is 1 and source is 1, then drain is 1”.  On the other hand, when source is 1 and gate is 0, drain attains ‘high impedance’. The reverse is true for PMOS.

Similarly, with the same logic, for an enhancement NMOS, “When Gate is 1 and source is 0, drain attains 0 potential”; similarly, “When Gate is 0 and source is 0, drain is 0”. The reverse is true for PMOS.

Source voltage	Gate voltage	Drain voltage for enhancement NMOS	Drain voltage for enhancement PMOS	Drain voltage for depletion NMOS	Drain voltage for depletion PMOS
0	0	Z	Z	0	0
0	1	0	Z	0	Z
1	0	Z	1	Z	1
1	1	Z	Z	1	1

Thus, we can say that it is due to the inherent properties of NMOS and PMOS that that they cannot be used to create negative level logic.

Setup checks and hold checks for flop-to-flop paths

In the post (Setup time and hold time – static timing analysis), we introduced setup and hold timing requirements and also discussed why these requirements exist. In this post, we will be discussing how these checks are applied for different cases for paths starting from and ending at flip-flops.

In present day designs, most of the paths (more than 95%) start from and end at flip-flops (exceptions are there like paths starting from and/or ending at latches). There can be flops which are positive edge triggered or negative edge triggered. Thus, depending upon the type of launching flip-flop and capturing flip-flop, there can be 4 cases as discussed below:

1)      Setup and hold checks for paths launching from positive edge-triggered flip-flop and being captured at positive edge-triggered flip-flop (rise-to-rise checks): Figure 1 shows a path being launched from a positive edge-triggered flop and being captured on a positive edge-triggered flop. In this case, setup check is on the next rising edge and hold check is on the same edge corresponding to the clock edge on which launching flop is launching the data.

Figure 1 : Timing path from positive edge flop to positive edge flop (rise to rise path)

Figure 2 below shows the setup and hold checks for positive edge-triggered register to positive edge-triggered register in the form of waveform. As is shown, setup check occurs at the next rising edge and hold check occurs at the same edge corresponding to the launch clock edge. For this case setup timing equation cab be given as:

            T_ck->q + T_prop + T_setup < T_period + T_{skew               (for setup check)}
And the equation for hold timing can be given as:

            T_ck->q + T_prop > T_hold + T_{skew                                  (for hold check)}

Where

        T_ck->q  : Clock-to-output delay of launch register

        T_prop : Maximum delay of the combinational path between launch and capture register

       T_hold : Hold time requirement of capturing register

       T_skew : skew between the two registers (Clock arrival at capture register - Clock arrival at launch register)

 

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window
                Start of data valid window = T_launch + T_hold
                End of data valid window = T_launch + T_period – T_setup

In other words, data at the input of capture register can toggle any time between (T_launch + T_hold) and (T_launch + T_period – T_setup).

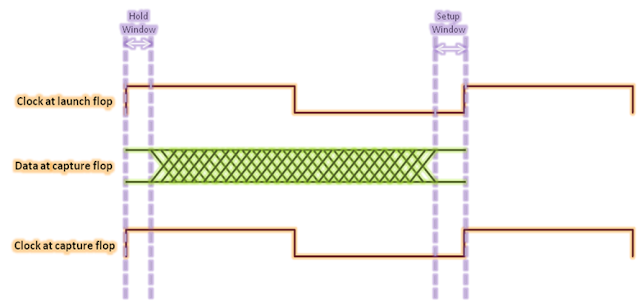Figure 3: Figure showing data valid window for rise-to-rise path

2)        Setup and hold checks for paths launching from positive edge-triggered flip-flop and being captured at negative edge-triggered flip-flop: In this case, both setup and hold check are half cycle checks; setup being checked on the next falling edge at the capture flop and hold on the previous falling edge of clock at the capture flop (data is launched at rising edge). Thus, with respect to (case 1) above, setup check has become tight and hold check has relaxed.

Figure 4: Timing path from positive edge flop to negative edge flop (Rise-to-fall path)

Figure 5 below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next falling edge and hold check occurs at the previous falling edge corresponding to the launch clock edge. The equation for setup check can be written, in this case, as:

            T_ck->q + T_prop + T_setup  < (T_period/2) + T_{skew                       (for setup check)}

And the equation for hold check can be written as:
            T_ck->q + T_prop + (T_period/2) > T_hold + T_{skew                         (for hold check)}

 

Figure 5: Setup and hold checks for rise-to-fall paths

Also, we show below the data valid and invalid windows. From this figure, 

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch – (T_period/2)+ T_hold

                End of data valid window = T_launch + (T_period/2) – T_setup

As we can see, the data valid window is spread evenly on both sides of launch clock edge.

 

Figure 6: Figure showing data valid window for rise-to-fall path

3)           Setup and hold checks for paths launching from negative edge-triggered flip-flop and being captured at positive edge-triggered flip-flop (rise-to-fall paths): This case is similar to case 2; i.e. both setup and hold checks are half cycle checks. Data is launched on negative edge of the clock, setup is checked on the next rising edge and hold on previous rising edge of the clock.

Figure 7: Timing path from negative edge flop to positive edge flop (fall-to-rise path)

Figure 8 below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next rising edge and hold check occurs at the previous rising edge corresponding to the launch clock edge.  The equation for setup check can be written, in this case, as:

            T_ck->q + T_prop + T_setup  < (T_period/2) + T_{skew                       (for setup check)}

And the equation for hold check can be written as:
            T_ck->q + T_prop + (T_period/2) > T_hold + T_{skew                         (for hold check)}

Figure 8: Setup and hold checks for fall to rise paths

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch – (T_period/2)+ T_hold

                End of data valid window = T_launch + (T_period/2) – T_setup

In this case too, data valid window spreads evenly on both the sides of launch clock edge.

 

Figure 9: Figure showing data valid window for fall-to-rise path

4)             Setup and hold checks for paths launching from negative edge-triggered flip-flop and being captured at negative edge-triggered flip-flop (fall-to-fall paths): The interpretation of this case is similar to case 1. Both launch and capture of data happen at negative edge of the clock. Figure 10 shows a path being launched from a negative edge-triggered flop and being captured on a negative edge-triggered flop. In this case, setup check is on the next falling edge and hold check is on the same edge corresponding to the clock edge on which launching flop is launching the data.

Figure 10: Path from negative edge flop to negative edge flop (fall to fall path)

Figure below shows the setup and hold checks in the form of waveforms. As is shown, setup check occurs at the next falling edge and hold check occurs at the same edge corresponding to the launch clock edge. 
The equation for setup check can be given as:

                T_ck->q + T_prop + T_setup < T_period + T_{skew                (for setup check)
And the equation for hold check can be given as:}

               T_ck->q + T_prop > T_hold + T_{skew                                                    (for hold check)} 

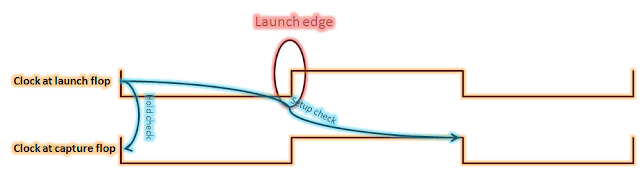Figure 11: Setup and hold check for fall-to-fall path

Also, we show below the data valid and invalid windows. From this figure,

                Data valid window = Clock period – Setup window – Hold window

                Start of data valid window = T_launch + T_hold

                End of data valid window = T_launch + T_period – T_setup

 

Figure 12: Figure showing data valid window for fall-to-fall path

Related posts:

• Setup time and hold time : static timing analysis
• Setup and hold checks for latch-to-reg and reg-to-latch paths
• Data checks: data setup and data hold checks
• On-chip variations
• Race conditions