2-input gates using 2:1 mux

Definition of a multiplexer: A 2^n-input mux has n select lines. It can be used to implement logic functions by implementing LUT (Look-Up Table) for that function. A 2-input mux can implement any 2-input function, a 4-input mux can implement any 3-input, an 8-input mux can implement any 4-input function, and so on. This property of muxes makes FPGAs implement programmable hardware with the help of LUT muxes. In this post, we will be discussing the implementation of 2-input AND, OR, NAND, NOR, XOR and XNOR gates using a 2-input mux.

2-input AND gate implementation using 2:1 mux: Figure 1 below shows the truth table of a 2-input AND gate. If we observe carefully, OUT equals '0' when A is '0'. And OUT follows B when A is '1'. So, if we connect A to the select pin of a 2:1 mux, AND gate will be implemented if we connect D0 to '0' and D1 to 'B'.

Figure 1: Truth table of AND gate

Figure 2 below shows the implementation of 2-input AND gate using a 2:1 multiplexer.

Figure 2: Implementation of AND gate using a 2:1 mux

2-input NAND gate using 2:1 mux: Figure 3 below shows the truth table of a 2-input NAND gate. If we observe carefully, OUT equals '1' when A is '0'. Similarly, when A is '1', OUT is B'. So, if we connect SEL pin of mux to A, D0 pin of mux to '1' and D1 to B', then it will act as a NAND gate.

Figure 3: Truth table of 2-input NAND gate

Figure 4 below shows the implementation of a 2-input NAND gate using 2:1 mux.

Figure 4: Implementation of 2-input NAND gate using 2:1 mux

2-input OR gate using 2x1 mux: Figure 5 below shows the truth table for a 2-input OR gate. If we observe carefully, OUT equals B when A is '0'. Similarly, OUT is '1' (or A), when A is '1'. So, we can make a 2:1 mux act like a 2-input OR gate, if we connect D0 pin to B and D1 pin to A, with select connected to A.

Figure 5: Truth table of 2-input OR gate

Figure 6 below shows the implementation of 2-input OR gate using a 2:1 multilpexer:

Figure 6: Implementation of 2-input OR gate using 2:1 mux

2-input NOR gate using 2x1 mux: Figure 7 below shows the truth table of a 2-input NOR gate. If we observe carefully, OUT equal B' when A is '0'. Similarly, OUT equals '0' when A is '1'. So, we can make a 2-input mux act like a 2-input NOR gate, if we connect SEL of mux to A, D0 to B' and D1 to '0'.

Figure 7: Truth table of 2-input NOR gate

Figure 8 shows the implementation of 2-input NOR gate using 2:1 mux.

Figure 8: Implementation of 2-input NOR gate using 2x1 mux

2-input XNOR gate using 2x1 mux: Figure 9 below shows the truth table of a 2-input XNOR gate. If we observe carefully, OUT equals B' when A is '0' and equals B when A is '1'. So, a 2-input XNOR gate can be implemented from a 2x1 mux, if we connect SEL pin to A, D0 to B' and D1 to B.

Figure 9: Truth table of 2-input XNOR gate

The implementation of 2-input XNOR gate using a 2x1 mux is as shown in figure 10.

Figure 10: Implementation of 2-input XNOR gate using 2x1 mux

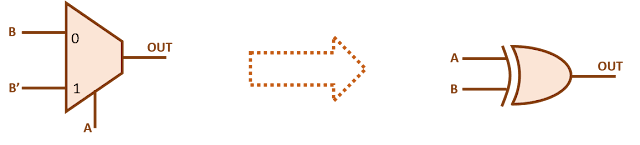
2-input XOR gate using 2x1 mux: Figure 11 shows the truth table for a 2-input XOR gate. If we observe carefully, OUT equals B when A is '0' and B' when A is '1'. So, a 2:1 mux can be used to implement 2-input XOR gate if we connect SEL to A, D0 to B and D1 to B'.

Figure 11: Truth table of 2-input XOR gate

Figure 12 shows the implementation of 2-input XOR gate using 2x1 mux.

Implementation of 2-input XOR gate using 2x1 mux

NOT gate using 2:1 mux: Figure 13 shows the truth table for a NOT gate. The only inverting path in a multiplexer is from select to output. To implement NOT gate with the help of a mux, we just need to enable this inverting path. This will happen if we connect D0 to '1' and D1 to '0'.

Figure 13: Truth table of NOT gate

Figure 14 shows the implementation of NOT gate using 2x1 mux:

Figure 14: Implementation of NOT gate using 2x1 mux

Multiplexer

Definition of mux: A multiplexer is a combinational circuit that selects one out of multiple input signals depending upon the state of select line. A 2^N:1 multiplexer with ‘N’ select lines can select 1 out of 2^N inputs. In other words, the multiplexer connects the output to one of its inputs based upon the value held at the select lines. A multiplexer (or commonly called as MUX) is also termed as data selector. Common functions of a multiplexer include concentrating the multiple data lines onto one single line. It can also be used as a data selector or clock selector.

Multiplexers can be categorized based upon the number of inputs:

• 2-input mux: A 2:1 mux has 2 data input lines and 1 select line. The state of select line decides which of the inputs propagates to the output. The truth table of 2x1 mux is given below. As it shows, when SEL is 1, OUT follows IN2 and when SEL is 0, OUT follows IN1.

Figure 1: Truth table of 2x1 mux

The logic circuit and symbol of 2x1 mux is shown in figure 2. Let us assume logical area of a 2:1 mux to be A.

Figure 2(a): Logic diagram of 2x1 mux                                               Figure 2(b): Schematic symbol of 2x1 mux

• 3-input mux: A 3:1 mux has 2 select lines and 3 inputs. As a mux with 2 select lines can represent at max 4 inputs, a 3:1 mux repeats some inputs for 2 combinations. The truth table for 3-input mux is given below. As can be seen, for SEL value "10" and "11", IN2 is selected at the output (this is one of the 3 possible scenarios, repetition of IN0 or IN1 is also possible).

Figure 3: Truth table for 3x1 mux

The schematic symbol and structural representation (in terms of 2x1 muxes) for 3:1 mux is shown in figure 4 below. As can be figured out, 1 3x1 mux can be built using 2 2x1 muxes.

Figure 4(a): Schematic symbol for 3x1 mux Figure                           4(b): Structural symbol for 3:1 mux using 2x1 muxes

• 4-input mux: A 4:1 mux has 2 select lines and 4 inputs. The truth table for 4x1 mux is shown below:

Figure 5: Truth table for 4:1 mux

Figure 6 below shows the schematic symbol and structural symbol of 4:1 mux using 2:1 muxes. As is evident, a 4:1 mux can be built from 3 2:1 muxes.

Figure 6(a): 4x1 mux schematic symbol     Figure 6(b): 4:1 mux structural representation with 2x1 muxes

• 8-input mux: An 8x1 mux has 3 select lines and 8 inputs. The truth table for 8x1 mux is shown below:

Figure 7: Truth table for 8:1 mux

The structural representation using 2x1 muxes, and schematic symbol for the same is as shown below in figure 8. An 8-input mux can be implemented using 7 2-input muxes.

Figure 8(a): Schematic symbol for 8x1 mux                    Figure 8(b): Structure of 8x1 mux  with 2x1 mux                                              

• 16-input mux: A 16x1 mux can be implemented from 15 2:1 muxes. It has 4 select lines and 16 inputs. Output follows one of the inputs depending upon the state of the select lines.

Also read:

• Build a 2-input XOR-XNOR gate using 2:1 mux
• Build a latch using 2:1 mux
• Multicycle paths - the architectural perspective
• Clock gating checks at a mux
• Implementing 3 and 4 variable functions using mux

Implement 3 and 4 variable function using 8:1 MUX

Three variable  function can be easily implemented using 8:1 multiplexer. connect 3 input lines to select lines of mux and connect 8 inputs of mux to logic 0 or 1 according to function output. For example, let us say Function is

                                      F(X,Y,Z) = Σ(0,1,3,6)

then X,Y,Z will be connected to select lines of Mux and I0 , I1, I3 and I6 will be connected to logic 1(VDD) and other will be connected to logic 0

For a 4 variable function, there are 16 possible combinations. To implement 4 variable function using 8:1 MUX, use 3 input as select lines of MUX and remaining 4th input and function will determine ith input of mux . Let us demonstrate it with an example :

                                  F(A,B,C,D) = Σ(1,5,7,9,10,11,12)

A	B	C	D	Decimal Equivalent	F
0	0	0	0	0	0
1	0	0	0	8	0
0	0	0	1	1	1
1	0	0	1	9	1
0	0	1	0	2	0
1	0	1	0	10	1
0	0	1	1	3	0
1	0	1	1	11	1
0	1	0	0	4	0
1	1	0	0	12	1
0	1	0	1	5	1
1	1	0	1	13	0
0	1	1	0	6	0
1	1	1	0	14	0
0	1	1	1	7	1
1	1	1	1	15	0

The 4 variable function represented using 8:1 mux

                                  ABar = ~A (inverted A)

As shown in figure, B,C,D are used as select lines and A will be used input  of Mux. from Truth table, if B,C,D  are 0 then output F is 0 irrespective of status of A so I0 = 0. For I5(BCD = 101) output depend upon A.

                                     for A = 0,  F  = 1
                                     for A = 1,  F =  0
                          Hence F = ~A (for BCD = 101)
                                    I4, (B = 1, C = 0, D = 0),  F = A
                                    I1, (B = 0, C =  0,D  = 1), F = 1 (irrespective of status of A)

similarly All other inputs can be inferred in the same way.  Thus we can conclude that to implement n variable function, we need 2^(n-1) to 1 MUX and an inverter. n-1 input lines shall be used as select lines and rest one will be used for input of MUX.

Also read:

• Binary to thermometer encoder
• Clock gating checks at a multiplexer
• Lockup latch - principle and application
• Carry look ahead adder
• Interesting problem - BCD multiply by 5 circuit