Binary multiplication process: A Binary Multiplier is a digital
circuit used in digital electronics to multiply two binary numbers and provide
the result as output. The method used to multiply two binary numbers is similar
to the method taught to school children for multiplying decimal numbers which
is based on calculating partial product, shifting them and adding them together.
Similar approach is used to multiply two binary numbers. Long multiplicand is
multiplied by 0 or 1 which is much easier than decimal multiplication as
product by 0 or 1 is 0 or same number respectively. Figure 1 below shows the block diagram of a 2-bit binary multiplier. The two numbers A1A0 and B1B0 are multiplied together to produce a 4-bit output P3P2P1P0. (The maximum product term can be 3 * 3 = 9, which is 1001, a 4-bit number).
 |
| Figure 1: 2-bit Binary Multiplier Block Diagram |
110 = 6
X 011 = 3
-----------------------------
-----------------------------
1 1 0 ;
110 X 1
1
1 0 x ; 110 X 1
0
0 0 x x ; 110 X 0
------------------------------
1 0 0 1 0 =18
Now, we have seen that
multiplying a number with binary ‘0’produces all zeroes, and with ‘1’ reproduces
the number. So, multiplying two binary numbers is a straightforward job. It can
be implemented without much difficulty using shifters, AND gates and adders.
2-bit binary multiplier circuit implementation: Let us implement a
two bit binary multiplier. Let the two binary numbers be A1A0
and B1B0. The multiplication table will, then, look as:
A1 A0
X
B1 B0
-------------------------------------------------------------------
B0A1 B0A0
B1A1 B1A0 x
-------------------------------------------------------------------
P3 P2 P1 P0
Thus, we get the partial products as:
P0 = A0*B0
P1 = A0*B1 xor A1 * B0 ; carry generated here goes
to next stage
P2 = A1*B1 xor (A0*B1) * (A1*B0)
P3 = A1*B1 and (A0*B1) * (A1*B0)
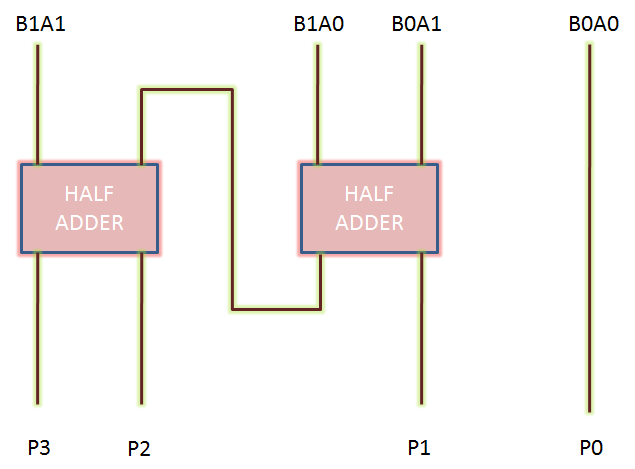 |
| Two-bit binary multiplier circuit diagram |
Thus, we can see that a 2-bit binary multiplier can be implemented using two half-adders only.
Characteristics of a binary multiplication: As mentioned above, a binary multiplier is used to multiply binary numbers. In general, the characteristics of binary multiplication are as follows:
Characteristics of a binary multiplication: As mentioned above, a binary multiplier is used to multiply binary numbers. In general, the characteristics of binary multiplication are as follows:
- To multiply two binary numbers, AND gates, shifters and adders are required.
- Product of N*M bit binary numbers in of (N+M) bits.
- N*M AND gates are required to generate partial products of two M*N bit binary numbers.
- Number of adders required = N+M-2
- Speed limiting factor here is to sum up partial products.
Also read: