Carry Look Ahead Adder

Carry look ahead adder definition: Carry Look Ahead Adder (CLA Adder) (also known as Carry Look Ahead Generator) is one of the digital circuits used to implement addition of binary numbers. It is an improvement over 'Ripple carry adder' circuit. In Ripple Carry adders, carry propagation time is the major speed limiting factor as it works on the basic mechanism to generate carries as we generally do while adding two numbers using pen and paper. A ripple carry adder may be supposed to be built of a series of 1-bit adders (generally known as a full adder in digital electronics). Thus, the speed of ripple carry adder is a direct function of number of bits. On the other hand, Carry Look Ahead adder solves this problem by calculating carry signals in advance based upon input bits and does not wait for the input signal to propagate through different adder stages. Hence, it implements the adder with reduced delay at the cost of more area (as large combinational logic is required to calculate the look ahead carry as compared to propagated carry).

Shown below is the truth table for a full adder (carry look ahead adder). A_i and B_i are two input bits and C_i is the carry input from the previous stage. S_i (Sum) and C_i+1 (Carry out for the next stage) are the outputs for the next stage of the adder. As is evident, carry signal is generated if at least two inputs of full adder are 1 i.e.

• When both bits Ai and Bi is 1 (regardless of Cin) OR
• When one of the two inputs (Ai or Bi) is 1 and carry-in (carry of previous stage) is 1

Ai	Bi	Ci	Si	Ci+1
0	0	0	0	0
0	0	1	1	0
0	1	0	1	0
0	1	1	0	1
1	0	0	1	0
1	0	1	0	1
1	1	0	0	1
1	1	1	1	1

The outputs of this full adder, when expressed in the form of a boolean expression can be written as a function of inputs as follows: 

          

        S_i = A_i xor B_i xor C_i

        C_i+1 = C_i(A_i xor B_i) + A_iB_i

Where S_i is the sum bit calculated for n^th adder stage and C_i+1 is the carry out from n^th stage and will act as input for n+1^th stage. For an N stage ripple carry adder, there is overhead of calculating the carry out of k^th stage before carry out of k+1^th stage can be calculated. If we go deeper into analysis, it comes out that c_k+1 is a function of c₀ and is discussed below. Let the intermediate outputs from a full adder stage be represented as Pi and Gi given as below:

          Pi = Ai xor Bi 

          Gi = Ai.Bi

          Si = Pi xor Ci

          Ci+1 = Ci.Pi + Gi

•  Gi is known as carry generate signal since carry (Ci+1)is generated whenever Gi= 1 regardless of Ci
• Pi is known as carry propagate signal since whenever Pi = 1, Ci+1 = Ci (when Pi=1, Gi = 0)

Thus, recursively replacing the values for Ci for each Ck, we can write the boolean expression of carry outputs of various stages in terms of C0 and Pk's as follows:

C1 = C0P0 + G0C2 = C1P1 + G1 = (C0P0+G0)P1 + G1 = C0P0P1 + P1G0 + G1C3 = C2P2 + G2 = (C0P0P1 + P1G0 + G1)P2+G2 = C0P0P1P2 + P2P1G0 + P2G1 +           G2C4 = C3P3 + G3 = (C0P0P1P2 + P2P1G0 + P2G1 + G2)P3 + G3 = C0P0P1P2P3 +             P3P2P1G0 + P3P2G1 + G2P3 + G3

Thus,

         C_i = F(P,G,C0)

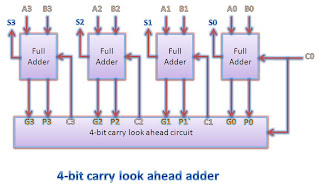4-bit carry look ahead adder block diagram

In other words, carry signal is a direct SOP (Sum of Products) expression of C₀ (usually 0) and input signals rather than its preceding carry signal. Let us illustrate taking a 4-bit adder as an example. This expression can be used to construct a carry look-ahead adder of any number of bits.

A 4 bit Carry Look Ahead (CLA) adder can be constructed with the help of following steps (Assuming T as the delay of a single 2-Input gate):

1. Generate All P and G internal signals. These can be generated simultaneously as C0 and all inputs are available. 
2. Generate all carry output signals (C1, C2, C3, C4). These will be valid after 3T time
3. Generate Sum signals S = P xor C. It will be valid after 4T time.

Thus, Sum signals will be valid after a delay of 4T. On the other hand, delay expression in case of ripple carry adder = (2n+2)T. Thus, for n =4, i.e. for 4 bit ripple carry adder, delay will be 10T.

For higher order addition, boolean expression of carry output becomes more complex. So, there is tradeoff between area and speed. For larger number of bits, increase in area is more than speed advantage obtained. Hence, Carry Look Ahead adders are usually implemented as 4-bit modules that are used to build larger size adders.

Below is a nice video that explains about carry look ahead adders (taken from youtube).