What is metastability: Metastability is a
phenomenon of unstable equilibrium in digital electronics in which the
sequential element is not able to resolve the state of the input signal; hence,
the output goes into unresolved state for an unbounded interval of time. Almost
always, this happens when data transitions very close to active edge of the
clock, hence, violating setup and hold requirements. Since, data makes
transition close to active edge of clock, the flop is not able to capture the
data completely. The flop starts to capture the data and output also starts to
transition. But, before output has changed its state, the input is cut-off from
the output as clock edge has arrived. The output is, then, left hanging between
state ‘0’ and state ‘1’. Theoretically, the output may remain in this state for
an indefinite period of time. But, given the time to settle down, the output
will eventually settle to either its previous state or the new state. Thus, the
effect of signal present at input of flop may not travel to the output of the
flop partly or completely. In other words, we can say that when a flip-flop
enters metastable state, one cannot predict its output voltage level after it
exits the metastability state nor when the output will settle to some stable
voltage level. The metastability failure is said to have occurred if the output
has not resolved itself by the time it must be available for use. Also, since,
the output remains in-between ‘0’ and ‘1’, which means both P-MOS and N-MOS are
not switched off. Hence, VDD is shorted to GND terminal making it cause a high
current to flow through as long as the output is hanging in-between.
Metastability example: Consider a CMOS inverter
circuit as shown below. The current vs voltage (we can also say power vs
voltage as VDD is constant) characteristics for this circuit are also shown. It
can be observed that output current is 0 for both input voltage levels; i.e.
‘0’ and ‘1’. As the voltage level is increased from ‘logic 0’, the current
increases. It attains its maximum value at ‘Vin’ somewhere near VDD/2. It again
starts decreasing as ‘Vin’ is increased further and again becomes 0 when ‘Vin’
is at ‘logic 1’. Thus, there is a local maxima for power consumption for CMOS
inverter. At this point, the device is in unstable equilibrium. As for CMOS
inverter, for other CMOS devices too, there lies ‘a local maxima’ at some value
of input voltage. We all know that for a flip-flop, the output stage is a
combinational gate (mostly an inverter). So, we can say that the output of the
flip-flop is prone to metastability provided right input level.
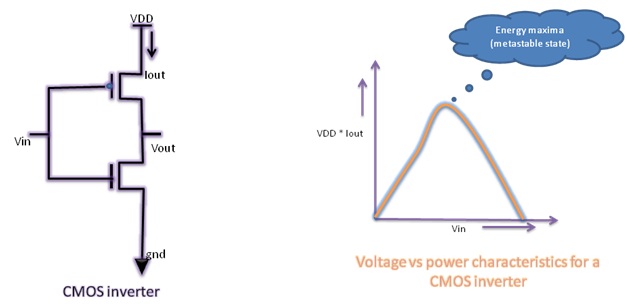 |
| Figure 1: Power characteristics of CMOS inverter |
As we now know that a
CMOS combinational gate has a point on its ‘voltage characteristic’ curve that
is quasi-stable, let us look at a CMOS latch from the same perspective. The
CMOS latch has a transmission gate followed by two inverters connected in
feedback loop. The voltage characteristic curves for the two inverters are
shown. The metastable point, here, lies where the two curves intersect as this
point is the resulting peak point of the ‘Superposition curve’ resulting from
the two individual curves. A latch goes into metastable state very frequently,
especially if the input is changing fast. But, this metastability is resolved
quickly as the output tends to go to one of its stable states. As a flop is
generally made by connecting two latches in master-slave configuration, the
flops are also prone to be metastable. The difference here is just that the
probability of a flip-flop being metastable is a lot less than latches as
‘flops are edge sensitive’ as compared to latches which are level sensitive.
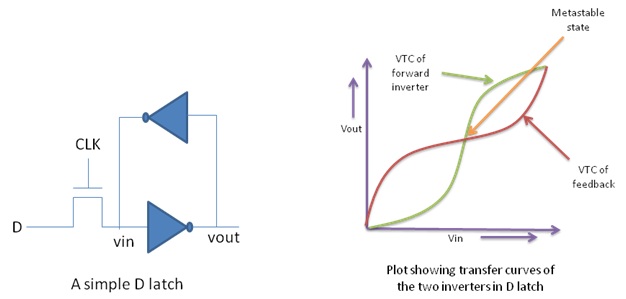 |
| Figure 2: Transfer curves of two inverters in a D-latch |
We have just came to know
that different elements are prone to metastability to different extents. There
is a measure to determine the extent to which an element is prone to
metastability failure. This is given by an interval known as ‘Mean Time Between
Failures’ (MTBF) and is a measure of how prone an element is to failure. It
gives the average time interval between two successive failures. The failure
rate is given as the reciprocal of MTBF.