Setup time

Definition of setup time: Setup time is defined as the minimum amount of time before arrival of clock's active edge so that it can be latched properly. In other words, each flip-flop (or any sequential element, in general) needs data to be stable for some time before arrival of clock edge such that it can reliably capture the data. This amount of time is known as setup time.

We can also link setup time with state transitions. We know that the data to be captured at the current clock edge was launched at previous clock edge by some other flip-flop. The data launched at previous clock edge must be stable  at least setup time before the current clock edge. So, adherence to setup time ensures that the data launched at previous edge is captured at the current clock edge reliably. In other words, setup time ensures that the design transitions to next state smoothly.

Figure 1: Setup time

Figure 1 shows that data is allowed to toggle prior to yellow dotted line. This yellow dotted line corresponds to setup time. The time difference between this line and active clock edge is termed as setup time. Data cannot toggle after this yellow dotted line for a duration known as setup-hold window. Occurrence of such an event will be termed as setup time violation. The consequence of setup time violation can be capture of wrong data or the sequential element (setup check violation) going into metastable state (setup time violation).

Figure 2: A positive level-sensitive D-latch

Latch setup time: Figure 2 shows a positive level-sensitive latch. If there is a toggling of data at the latch input close to negative edge (while the latch is closing), there will be an uncertainty as if data will be capture reliably or not. For data to be captured reliably, it has to be available at the input of loop transmission gate at the arrival of closing clock edge. To be able to present at NodeD at the closing edge, it must be there at latch input some time prior to the clock edge. This time in reaching from latch input to NodeD is termed as setup time for this latch.

Flip-flop setup time: Figure 3 below shows a master-slave negative edge-triggered D flip-flop using transmission gate latches. This is the most popular configuration of a flip-flop used in today's designs. Let us get into the details of setup time for this flip-flop. For this flip-flop to capture data reliably, the data must be present at nodeF at the arrival of negative edge of clock. So, data must travel NodeA -> NodeB -> NodeC -> NodeD -> NodeE -> NodeF before clock edge arrives. To reach NodeF at the closing edge of latch1, data should be present at NodeA at some earlier time. This time taken by data to reach NodeF is the setup time for flip-flop under consideration (assuming CLK and CLK' are present instantaneously. If that is not the case, it will be accounted for accordingly). We can also say that the setup time of flip-flop is, in a way, setup time of master latch.

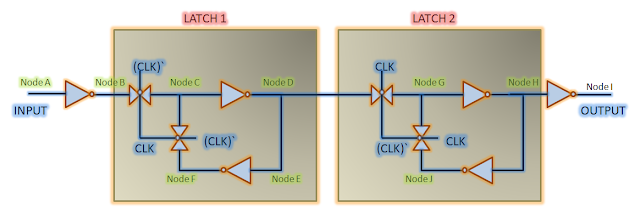Figure 3: D-flip flop

Programming problem: Synthsizable filter design in C++

Problem statement: Develop a synthesizable C/C++ function which is capable of performing image filtering. The filtering operation is defined by following equation:

// B -> filtered image

// A -> Input image

// h -> filter coefficients

int filter_func() {

                const int L = 1;

                const int x_size = 255;

                const int y_size = 255;

                int A_image[x_size][y_size];

                int B_image[x_size][y_size];

                int h[2*L+1][2*L+1];

                // Initializing the filtered image

                for (int i = 0; i < x_size; i++) {

                                for (int j = 0; j < y_size; j++) {

                                                B_image[i][j] = 0;

                                }

                }

                for (int i = 0; i < x_size; i++) {

                                for (int j = 0; j < y_size; j++) {

                                                for (int l = -L; l <= L; l++) {

                                                                for (int k = -L; k <= L; k++) {

                                                                                B_image[i][j] = B_image[i][j] + A_image[i-k][j-l]*h[k+L][l+L];

                                                                }

                                                }

                                }

                }

}

Hope you’ve found this post useful. Let us know what you think in the comments.