What is liberty format: Liberty format is an industry standard format used to describe library cells of a particular technology. A cell could be a standard cell, IO Buffer, complex IP etc. Library cell description contains a lot of information like timing information, power estimation, other several attributes like area, functionality, operating condition etc. Speaking more technically, liberty format is a format to represent timing and power properties of black boxes (which we cant descend into). Liberty is an ASCII format, usually represented in a text file with extension ".lib". In this section, we will discuss timing aspects (delay and transition times) related to liberty format.
How is liberty file populated with data: The cells represented through liberty files are first simulated under a variety of conditions representative of actual design conditions that the cell may be exposed to. This process is known as characterization of library cells. As a very simple example, the delay of an inverter depends upon the input transition time and output load capacitance seen by it. The inverter will be characterized for a range of input transitions and output load capacitances. This characterization data, will then, be put into liberty in the form of a look-up table representing delay values at different transition times and load values.
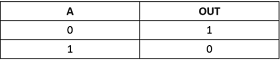
To understand the different constructs related to timing in liberty file, let us take example of inverter. Rising transition at the input of inverter produces falling transition at the output of inverter and vice-versa. Hence there are two types of delay :
- Rise delay : It is the propagation delay (see definition) between output and input when output changes from 0 to 1.
- Output fall delay : It is the propagation delay between output and input when output is changing from 1 to 0.
In the real world, signal does not change its state from 0 to 1 or 1 to 0 abruptly. It takes some time to change its state. Hence, delay is measured based upon the threshold points. Threshold points in the liberty file are specified as below:
# threshold point of input falling edge
input_threshold_pct_fall : 50.0 ;
# threshold point of input rising edge
input_threshold_pct_rise : 50.0 ;
#threshold point of output falling edge
output_threshold_pct_fall : 50.0 ;
#threshold point of output rising edge
output_threshold_pct_rise : 50.0 ;
NOTE : these values are in percentage. e.g. If vdd is 5v then all of the above values will be 2.5.
So, Output rise delay is time difference between output_threshold_pct_rise and input_threshold_pct fall. Similarly Output fall delay is time difference between output_threshold_pct_fall and input_threshold_pct_rise.
Transition time : Time it takes for a signal to changes its state from one level to another level. Transition time is represented in terms of slew in liberty. Actually slew is inversely proportional to transition time. More the transition time, lesser is the slew rate and vice-versa. As we know that
voltage transition at the output is :
V = Vdd * [ 1 - e^ ( -t/(RC ) ) ]
As Voltage equation is exponential, the voltage waveform is asymptotic at ends It is difficult to determine the exact start and end point of transition hence transition time is defined in terms of threshold values as follow :
# lower threshold point for falling edge
slew_lower_threshold_pct_fall : 30;
# upper threshold point for falling edge
slew_upper_threshold_pct_fall : 30;
# lower threshold point for rising edge
slew_lower_threshold_pct_rise : 70;
# upper threshold point for rising edge
slew_upper_threshold_pct_rise : 70;