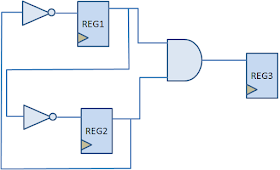
Problem: There is an 4-bit shift register with parallel read and write capability as shown in the diagram. We need to find out an opportunity to clock gate the module.
Mode selection bits ("S1" and "S0") are controlling the operation of this shift register with following settings:
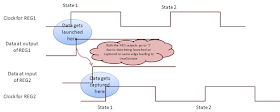
Can you relate the timing of S1 and S0? Should they be coming from positive edge-triggered flip-flop or negative edge-triggered flip-flop? Clock gating checks explains the timing of clock gating signals with respect to clock.
Also read:
Solution: From the basics of clock gating, we know that if the stae of a flip-flop is not chaging, there lies an opportunity to gate its clock. Observing the table, we see that state of all flip-flops does not change when "S1,S0" are either "00" or "11". So, when mode selection bits are corresponding to these values, we can gate the clock to this shift register. Or, we can say that clock to the module should reach only when (S1 xor S0) is equal to 1.
Can you relate the timing of S1 and S0? Should they be coming from positive edge-triggered flip-flop or negative edge-triggered flip-flop? Clock gating checks explains the timing of clock gating signals with respect to clock.
Also read: